
【题目】如图所示,平面ABC⊥平面BCDE,BC∥DE, ![]() ,BE=CD=2,AB⊥BC,M,N分别为DE,AD中点.
,BE=CD=2,AB⊥BC,M,N分别为DE,AD中点. 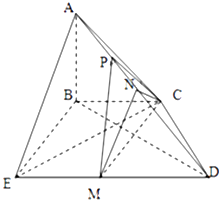
(1)证明:平面MNC⊥平面BCDE;
(2)若EC⊥CD,点P为棱AD的三等分点(近A),平面PMC与平面ABC所成锐二面角的余弦值为 ![]() ,求棱AB的长度.
,求棱AB的长度.
【答案】
(1)证明:连结BM,ON,
由题意四边形BMDC是菱形,∴O是BD中点,
∵N是AD中点,∴ON∥AB,
∵AB⊥BC,平面ABC⊥平面BCDE,∴AB⊥平面BCDE,
∴ON⊥平面BCDE,
∵ON平面MNC,∴平面MNC⊥平面BCDE
(2)解:以C为原点,CE为x轴,CD为y轴,过C作平面BCDE的垂线为z轴,建立空间直角坐标系,
设A( ![]() ,﹣1,t),(t>0)由题意D(0,2,0),P(
,﹣1,t),(t>0)由题意D(0,2,0),P( ![]() ,0,
,0, ![]() ),E(2
),E(2 ![]() ,0,0),
,0,0),
D(0,2,0),M( ![]() ),B(
),B( ![]() ,0),C(0,0,0),
,0),C(0,0,0),
![]() =(
=( ![]() ,0,
,0, ![]() ),
), ![]() =(
=( ![]() ),
), ![]() =(
=( ![]() ,0),
,0), ![]() =(
=( ![]() ),
),
设平面PMC的法向量 ![]() =(x,y,z),
=(x,y,z),
则 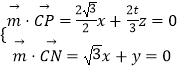 ,取x=
,取x= ![]() ,得
,得 ![]() =(
=( ![]() ,﹣3,﹣
,﹣3,﹣ ![]() ),
),
设平面ABC的法向量 ![]() =(a,b,c),
=(a,b,c),
则 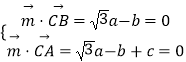 ,取a=
,取a= ![]() ,得
,得 ![]() =(
=( ![]() ,0),
,0),
∵平面PMC与平面ABC所成锐二面角的余弦值为 ![]() ,
,
∴|cos< ![]() >|=
>|= ![]() =
= ![]() =
= ![]() ,解得t=3.
,解得t=3.
∴棱AB的长度为3.
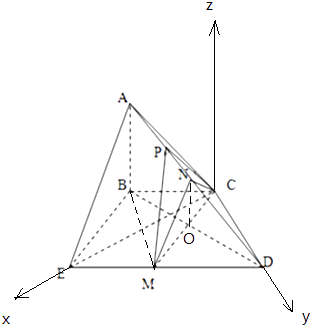
【解析】(1)连结BM,ON,推导出ON∥AB,AB⊥平面BCDE,从而ON⊥平面BCDE,由此能证明平面MNC⊥平面BCDE.(2)以C为原点,CE为x轴,CD为y轴,过C作平面BCDE的垂线为z轴,建立空间直角坐标系,利用向量法能求出棱AB的长度.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两地相距200千米,汽车从甲地匀速行驶到乙地,速度不得超过50千米/时.已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比,比例系数为0.02;固定部分为50(元/时).
(1)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出定义域;
(2)用单调性定义证明(1)中函数的单调性,并指出汽车应以多大速度行驶可使全程运输成本最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,2016年“双十”天猫总成交金额突破1207亿元.某购物网站为优化营销策略,对11月11日当天在该网站进行网购消费且消费金额不超过1000元的1000名网购者(其中有女性800名,男性200名)进行抽样分析.采用根据性别分层抽样的方法从这1000名网购者中抽取100名进行分析,得到下表:(消费金额单位:元)
女性消费情况:
消费金额 |
|
|
|
|
|
人数 | 5 | 10 | 15 | 47 |
|
男性消费情况:
消费金额 |
|
|
|
|
|
人数 | 2 | 3 | 10 |
| 2 |
(1)计算![]() ,
,![]() 的值;在抽出的100名且消费金额在
的值;在抽出的100名且消费金额在![]() (单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者恰好是一男一女的概率;
(单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者恰好是一男一女的概率;
(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写![]() 列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
女性 | 男性 | 总计 | |
网购达人 | |||
非网购达人 | |||
总计 |
附:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|+|x﹣a|.
(1)当a=2时,求不等式f(x)≥4的解集;
(2)不等式f(x)<4的解集中的整数有且仅有1,2,3,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() 底面
底面![]() ,
, ![]() 是棱
是棱![]() 的中点,
的中点,
且![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)如果![]() 是棱
是棱![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条直线l1:y=a和l2:y= ![]() (其中a>0),若直线l1与函数y=|log4x|的图象从左到右相交于点A,B,直线l2与函数y=|log4x|的图象从左到右相交于点C,D.记线段AC和BD在x轴上的投影长度分别为 m,n.令f(a)=log4
(其中a>0),若直线l1与函数y=|log4x|的图象从左到右相交于点A,B,直线l2与函数y=|log4x|的图象从左到右相交于点C,D.记线段AC和BD在x轴上的投影长度分别为 m,n.令f(a)=log4 ![]() .
.
(1)求f(a)的表达式;
(2)当a变化时,求出f(a)的最小值,并指出取得最小值时对应的a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com