
【题目】在某中学举行的环保知识竞赛中,将三个年级参赛的学生的成绩进行整理后分为5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组,已知第二小组的频数是40,则成绩在80~100分的学生人数是( )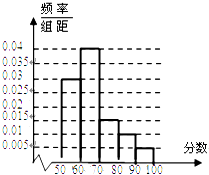
A.15
B.18
C.20
D.25
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:x∈R,x2+1>m;命题q:指数函数f(x)=(3﹣m)x是增函数.若“p∧q”为假命题且“p∨q”为真命题,则实数m的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为正数,给出下列命题:
①若a2﹣b2=1,则a﹣b<1;
②若 ![]() ﹣
﹣ ![]() =1,则a﹣b<1;
=1,则a﹣b<1;
③ea﹣eb=1,则a﹣b<1;
④若lna﹣lnb=1,则a﹣b<1.
期中真命题的有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,(e为自然对数的底数,a,b∈R),若f(x)在x=0处取得极值,且x﹣ey=0是曲线y=f(x)的切线.
,(e为自然对数的底数,a,b∈R),若f(x)在x=0处取得极值,且x﹣ey=0是曲线y=f(x)的切线.
(1)求a,b的值;
(2)用min{m,n}表示m,n中的最小值,设函数 ![]() ,若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
,若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,M,N分别是AB,PC的中点,若ABCD是平行四边形.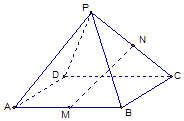
(1)求证:MN∥平面PAD.
(2)若PA=AD=2a,MN与PA所成的角为30°.求MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月1日起全国统一实施全面的两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取70后80后作为调查对象,随机调查了100人并对调查结果进行统计,70后不打算生二胎的占全部调查人数的15%,80后打算生二胎的占全部被调查人数的45%,100人中共有75人打算生二胎.
(1)根据调查数据,判断是否有90%以上把握认为“生二胎与年龄有关”,并说明理由;
(2)以这100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,记其中打算生二胎的人数为X,求随机变量X的分布列,数学期望E(X)和方差D(X). 参考公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
( ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来蓬勃发展新机遇,2016年双11期间,某网络购物平台推销了A,B,C三种商品,某网购者决定抢购这三种商品,假设该名网购者都参与了A,B,C三种商品的抢购,抢购成功与否相互独立,且不重复抢购同一种商品,对A,B,C三件商品抢购成功的概率分别为a,b, ![]() ,已知三件商品都被抢购成功的概率为
,已知三件商品都被抢购成功的概率为 ![]() ,至少有一件商品被抢购成功的概率为
,至少有一件商品被抢购成功的概率为 ![]() .
.
(1)求a,b的值;
(2)若购物平台准备对抢购成功的A,B,C三件商品进行优惠减免,A商品抢购成功减免2百元,B商品抢购成功减免4比百元,C商品抢购成功减免6百元.求该名网购者获得减免总金额(单位:百元)的分别列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosx(sinx﹣cosx)+m(m∈R),将y=f(x)的图象向左平移 ![]() 个单位后得到y=g(x)的图象,且y=g(x)在区间
个单位后得到y=g(x)的图象,且y=g(x)在区间 ![]() 内的最大值为
内的最大值为 ![]() .
.
(1)求实数m的值;
(2)在△ABC中,内角A、B、C的对边分别是a、b、c,若 ![]() ,且a+c=2,求△ABC的周长l的取值范围.
,且a+c=2,求△ABC的周长l的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com