
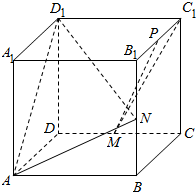
分析 对3个命题分别进行判断,即可得出结论.
解答 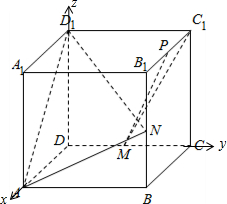 解:①如图,建立空间直角坐标,则A(a,0,0),N(a,a,$\frac{1}{2}$a),M(0,$\frac{1}{2}$a,0),C1(0,a,a)
解:①如图,建立空间直角坐标,则A(a,0,0),N(a,a,$\frac{1}{2}$a),M(0,$\frac{1}{2}$a,0),C1(0,a,a)
∴$\overrightarrow{{C}_{1}M}$=(0,-$\frac{1}{2}$a,-a),$\overrightarrow{AN}$=(0,a,$\frac{1}{2}$a)
∴cos<$\overrightarrow{{C}_{1}M}$,$\overrightarrow{AN}$>=$\frac{-{a}^{2}}{\frac{\sqrt{5}}{2}a•\frac{\sqrt{5}}{2}a}$=-$\frac{4}{5}$
∴异面直线C1M与AN所成角的正弦值为$\frac{3}{5}$,正确;
②设平面AD1N的法向量为$\overrightarrow{m}$=(x,y,z),则
∵$\overrightarrow{A{D}_{1}}$=(-a,0,a),$\overrightarrow{AN}$=(-a,$\frac{1}{2}$a,0),
∴$\left\{\begin{array}{l}{-ax+az=0}\\{-ax+\frac{1}{2}ay=0}\end{array}\right.$,∴$\overrightarrow{m}$=(1,2,1),
同理平面MC1P的法向量为$\overrightarrow{n}$=(4,2,-1),
∴$\overrightarrow{m}$•$\overrightarrow{n}$=4+4-1=7,∴平面MC1P⊥平面AD1N,不正确;
③设点A1到平面MC1P的距离等于h,${S}_{△M{C}_{1}P}$=$\frac{1}{2}•\frac{a}{2}•\frac{\sqrt{5}}{2}a$=$\frac{\sqrt{5}}{8}$a2,${S}_{△{A}_{1}{C}_{1}P}$=$\frac{1}{2}•\frac{a}{2}•a$=$\frac{{a}^{2}}{4}$,
∴由等体积可得$\frac{1}{3}•\frac{\sqrt{5}}{8}{a}^{2}h=\frac{1}{3}•\frac{{a}^{2}}{4}•a$,
∴h=$\frac{2\sqrt{5}}{5}$a.故不正确.
故答案为:①
点评 本题考查异面直线C1M与AN所成角的正弦值,平面与平面垂直,考查点到平面的距离,考查学生分析解决问题的能力,知识综合性强.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{10}}{5}$ | B. | $\frac{18}{5}$ | C. | $\frac{16}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=2x′}\\{y=\frac{1}{3}y′}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x′=2x}\\{y′=\frac{1}{3}y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2x′}\\{y=3y′}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x′=2x}\\{y′=3y}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{π}{4}$-$\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
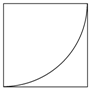 一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于$\frac{\sqrt{15}}{3}$πcm3.
一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于$\frac{\sqrt{15}}{3}$πcm3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
| 态度 年龄 | 赞成 | 不赞成 | 总计 |
| 中青年 | |||
| 中老年 | |||
| 总计 |
| X2 | ≤2.706 | >2.706 | >3.841 | >6.635 |
| A、B关联性 | 无关联 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 求数列{$\frac{1}{n}$}的前11项和(n∈N*) | B. | 求数列{$\frac{1}{2n}$}的前11项和(n∈N*) | ||
| C. | 求数列{$\frac{1}{n}$}的前12项和(n∈N*) | D. | 求数列{$\frac{1}{2n}$的前12项和(n∈N*) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com