
【题目】平面四边形![]() 中,
中, ![]() ,
, ![]() 为等边三角形,现将
为等边三角形,现将![]() 沿
沿![]() 翻折得到四面体
翻折得到四面体![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.


(Ⅰ)求证:四边形![]() 为矩形;
为矩形;
(Ⅱ)当平面![]() 平面
平面![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析 (Ⅱ)![]()
【解析】【试题分析】(1)先运用三角形中位线定理证得四边形![]() 为平行四边形,再借助等边三角形的性质及线面垂直的判定定理证明
为平行四边形,再借助等边三角形的性质及线面垂直的判定定理证明![]() ,进而证明
,进而证明![]() ,从而证明四边形
,从而证明四边形![]() 为矩形;(2)先依据题设条件及面面垂直的性质定理证明
为矩形;(2)先依据题设条件及面面垂直的性质定理证明![]() 平面
平面![]() ,再建立空间直角坐标系,运用空间向量的数量积公式求出平面
,再建立空间直角坐标系,运用空间向量的数量积公式求出平面![]() 的一个法向量
的一个法向量![]() .进而求出直线
.进而求出直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值:
的正弦值:
解:(Ⅰ)∵点![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() 且
且![]() ,
,
∴四边形![]() 为平行四边形.
为平行四边形.
取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
∵![]() 为等腰直角三角形,
为等腰直角三角形, ![]() 为正三角形,
为正三角形,
∴![]() ,
,
∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
由![]() 且
且![]() 可得
可得![]() ,
,
∴四边形![]() 为矩形.
为矩形.

(Ⅱ)由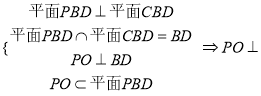 平面
平面![]()
分别以![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() .
.
依题意,设![]() ,则
,则![]() ,
,
∴![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,则有
的一个法向量,则有
令![]() ,则
,则![]() .
.
∴直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值
的正弦值
 .
.


科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点在抛物线
的焦点在抛物线![]() 上,点
上,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(Ⅰ)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
(Ⅱ)过点![]() 作抛物线
作抛物线![]() 的两条切线,
的两条切线, ![]() 、
、![]() 分别为两个切点,求
分别为两个切点,求![]() 面积的最小值.
面积的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=aex+ ![]() +b(a>0).
+b(a>0).
(1)求f(x)在[0,+∞)上的最小值;
(2)设曲线y=f(x)在点(2,f(2))的切线方程为3x﹣2y=0,求a、b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为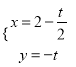 ,(
,( ![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() ,若点
,若点![]() 是直线
是直线![]() 上一动点,过点
上一动点,过点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在实数集R上的可导函数f(x),满足f(x+2)是奇函数,且 ![]() >2,则不等式f(x)>
>2,则不等式f(x)> ![]() x﹣1的解集是( )
x﹣1的解集是( )
A.(﹣∞,2)
B.(2,+∞)
C.(0,2)
D.(﹣∞,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=sin2x+ ![]() sinxcosx+
sinxcosx+ ![]() ,x∈R,
,x∈R,
(1)求函数f(x)的最小正周期T及在[﹣π,π]上的单调递减区间;
(2)若关于x的方程f(x)+k=0,在区间[0, ![]() ]上且只有一个实数解,求实数k的取值范围.
]上且只有一个实数解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=2|x﹣m|﹣1(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( )
A.a<b<c
B.c<a<b
C.a<c<b
D.c<b<a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com