已知不等式ax2+bx+c>0的解集为(1,t),记函数f(x)=ax2+(a-b)x-c.
(1)求证:函数y=f(x)必有两个不同的零点.
(2)若函数y=f(x)的两个零点分别为m,n,求|m-n|的取值范围.
(3)是否存在这样实数的a、b、c及t,使得函数y=f(x)在[-2,1]上的值域为[-6,12].若存在,求出t的值及函数y=f(x)的解析式;若不存在,说明理由.
解:(1)由题意知,∵
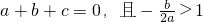
,∴
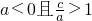
,∴ac>0.
对于函数f(x)=ax
2+(a-b)x-c.有△=(a-b)
2+4ac>0,∴f(x)必有2个不同零点.
(2)
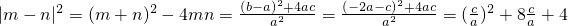
由不等式ax
2+bx+c>0的解集为(1,t)可知,ax
2+bx+c=0的两个解分别为1和t(t>1),
由韦达定理有
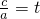
,∴|m-n|
2=t
2+8t+4=(t+4)
2-12,t∈(1,+∞),∴|m-n|
2>5
2-12=13,∴
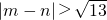
,
即|m-n|的取值范围为(

,+∞).
(3)假设存在满足题意的实数a、b、c及t,∴

=a[x
2+(2+t)x-t](t≥1),∴f(x)的对称轴为
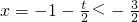
,∴f(x)在[-2,1]的最小值为f(1)=3a=-6,则a=-2.
要使函数y=f(x)在[-2,1]上的值域为[-6,12],只要f(x)
max=12即可.
①若
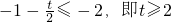
时,f(x)
max=f(-2)=123,则有6t=12,∴t=24.
此时,a=-2,b=6,c=-4,t=2,∴f(x)=-2x
2-8x+4.
②若
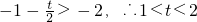
,此时,
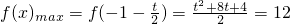
,∴t=2(舍去),或t=-10(舍去 ).
综上所述:当a=-2,b=6,c=-4,t=2时,函数y=f(x)在[-2,1]上的值域为[-6,12],此时函数的表达式为f(x)=-2x
2-8x+4.
分析:(1)由题意可得ac>0,对于函数f(x)=ax
2+(a-b)x-c,由△=(a-b)
2+4ac>0,可得f(x)必有2个不同零点.
(2)化简|m-n|
2等于
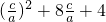
,由不等式ax
2+bx+c>0的解集为(1,t),可得有
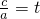
,化简|m-n|
2 =(t+4)
2-12,t∈(1,+∞),利用二次函数的性质
可得|m-n|
2的范围,从而求得|m-n|的取值范围.
(3)假设存在满足题意的实数a、b、c及t,化简f(x)等于a[x
2+(2+t)x-t](t≥1),f(x)的对称轴为
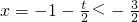
,分
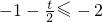
和
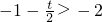
两种情况,
根据函数y=f(x)在[-2,1]上的值域为[-6,12],分别求得a、b、c及t的值,从而得到结果.
点评:本题主要考查函数的零点的定义,二次函数的性质应用,求二次函数在闭区间上的最值,体现了分类讨论的数学思想,属于基础题.

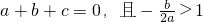 ,∴
,∴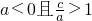 ,∴ac>0.
,∴ac>0.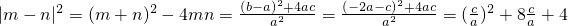
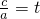 ,∴|m-n|2=t2+8t+4=(t+4)2-12,t∈(1,+∞),∴|m-n|2>52-12=13,∴
,∴|m-n|2=t2+8t+4=(t+4)2-12,t∈(1,+∞),∴|m-n|2>52-12=13,∴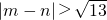 ,
, ,+∞).
,+∞).
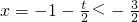 ,∴f(x)在[-2,1]的最小值为f(1)=3a=-6,则a=-2.
,∴f(x)在[-2,1]的最小值为f(1)=3a=-6,则a=-2.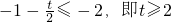 时,f(x)max=f(-2)=123,则有6t=12,∴t=24.
时,f(x)max=f(-2)=123,则有6t=12,∴t=24.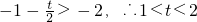 ,此时,
,此时,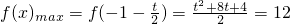 ,∴t=2(舍去),或t=-10(舍去 ).
,∴t=2(舍去),或t=-10(舍去 ).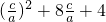 ,由不等式ax2+bx+c>0的解集为(1,t),可得有
,由不等式ax2+bx+c>0的解集为(1,t),可得有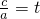 ,化简|m-n|2 =(t+4)2-12,t∈(1,+∞),利用二次函数的性质
,化简|m-n|2 =(t+4)2-12,t∈(1,+∞),利用二次函数的性质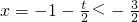 ,分
,分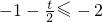 和
和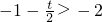 两种情况,
两种情况,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案