
【题目】已知双曲线![]() 的离心率为
的离心率为![]() ,且焦点到渐近线的距离为
,且焦点到渐近线的距离为![]() .
.
(1)求双曲线![]() 的标准方程;
的标准方程;
(2)若以![]() 为斜率的直线
为斜率的直线![]() 与双曲线
与双曲线![]() 相交于两个不同的点
相交于两个不同的点![]() ,
,![]() ,且线段
,且线段![]() 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 | 总计 |
男 | 10 | 8 | 7 | 3 | 2 | 15 | 45 |
女 | 5 | 4 | 6 | 4 | 6 | 30 | 55 |
总计 | 15 | 12 | 13 | 7 | 8 | 45 | 100 |
(1)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,能否在犯错误概率不超过0.005的前提下,认为是否为“移动支付活跃用户”与性别有关?
(2)把每周使用移动支付6次及6次以上的用户称为“移动支付达人”,视频率为概率,在我市所有“移动支付达人”中,随机抽取4名用户.
①求抽取的4名用户中,既有男“移动支付达人”又有女“移动支付达人”的概率;
②为了鼓励男性用户使用移动支付,对抽出的男“移动支付达人”每人奖励300元,记奖励总金额为X,求X的分布列及均值.
附公式及表如下:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() :
:![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 相切于点
相切于点![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)已知直线![]() :
:![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
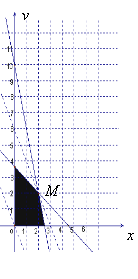
【题目】(本小题满分13分)某县一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨、硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨、硝酸盐15吨.先库存磷酸盐10吨、硝酸盐66吨,在此基础上生产这两种混合肥料.若生产1车皮甲种肥料产生的利润为10000元;生产1车皮乙种肥料产生的利润为5000元.那么分别生产甲、乙两种肥料各多少车皮能产生最大的利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】车工刘师傅利用数控车床为某公司加工一种高科技易损零件,对之前加工的100个零件的加工时间进行统计,结果如下:
加工1个零件用时 | 20 | 25 | 30 | 35 |
频数(个) | 15 | 30 | 40 | 15 |
以加工这100个零件用时的频率代替概率.
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘师傅准备给几个徒弟做一个加工该零件的讲座,用时40分钟,另外他打算在讲座前、讲座后各加工1个该零件作示范.求刘师傅讲座及加工2个零件作示范的总时间不超过100分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第16届亚运会在中国广州进行,为了搞好接待工作,组委会招幕了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有![]() 人和
人和![]() 人喜爱运动,其余人不喜爱运动.
人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下![]() 列联表:
列联表:
喜爱运动 | 不喜爱运动 | 总计 | |
男 |
|
| |
女 |
|
| |
总计 |
|
(2)根据列联表的独立性检验,能否在犯错误的概率不超过![]() 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
附:
|
|
|
|
|
|
|
|
|
|
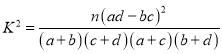 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,将
,将![]() 逆时针旋转
逆时针旋转![]() 后,与曲线
后,与曲线![]() 相交于点
相交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com