
【题目】设D是圆O:x2+y2=16上的任意一点,m是过点D且与x轴垂直的直线,E是直线m与x轴的交点,点Q在直线m上,且满足2|EQ|![]() |ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
|ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程.
(2)已知点P(2,3),过F(2,0)的直线l交曲线C于A,B两点,交直线x=8于点M.判定直线PA,PM,PB的斜率是否依次构成等差数列?并说明理由.
【答案】(1)![]() 1,(2)成等差数列
1,(2)成等差数列
【解析】
(1)由题意设Q(x,y),D(x0,y0),根据2|EQ|![]() |ED|Q在直线m上,则椭圆的方程即可得到;
|ED|Q在直线m上,则椭圆的方程即可得到;
(2)设出直线l的方程,和椭圆方程联立,利用根与系数的关系得到k1+k3,并求得k2的值,由k1+k3=2k2说明直线PA,PM,PB的斜率成等差数列.
解:(1)设Q(x,y),D(x0,y0),∵2|EQ|![]() |ED|,Q在直线m上,
|ED|,Q在直线m上,
∴x0=x,|y0|=|![]() y|.①
y|.①
∵点D在圆x2+y2=16上运动,
∴x02+y02=16,
将①式代入②式即得曲线C的方程为x2![]() y2=16,即
y2=16,即![]() 1,
1,
(2)直线PA,PM,PB的斜率成等差数列,证明如下:
由(1)知椭圆C:3x2+4y2=48,
直线l的方程为y=k(x﹣2),
代入椭圆方程并整理,得(3+4k2)x2﹣16k2x+16k2﹣48=0.
设A(x1,y1),B(x2,y2),直线PA,PM,PB的斜率分别为k1,k2,k3,
则有x1+x2![]() ,x1x2
,x1x2![]() ,
,
可知M的坐标为(8,6k).
∴k1+k3![]()
=2k﹣3![]() 2k﹣3
2k﹣3![]() 2k﹣1,
2k﹣1,
2k2=2![]() 2k﹣1.
2k﹣1.
∴k1+k3=2k2.
故直线PA,PM,PB的斜率成等差数列.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】随着互联网经济不断发展,网上开店销售农产品的人群越来越多,网上交易额也逐年增加,某一农户农产品连续五年的网银交易额统计表,如下所示:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
网上交易额 | 5 | 6 | 7 | 8 | 10 |
经研究发现,年份与网银交易额之间呈线性相关关系,为了计算的方便,农户将上表的数据进行了处理,![]() ,得到如表:
,得到如表:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程.求出![]() 关于
关于![]() 的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
(附:在线性回归方程![]() 中,
中,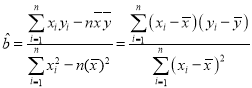 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体![]() 中,四边形
中,四边形![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 上的动点.
上的动点.
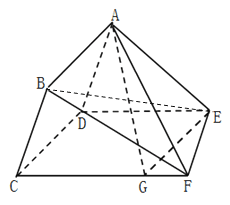
(Ⅰ)当![]() 时,求证
时,求证![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)若二面角![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0与1两个数字随机填入如图所示的5个格子里,每个格子填一个数字,并且从左到右数,不管数到哪个格子,总是1的个数不少于0的个数,则这样填法的概率为__________.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于![]() ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35B.0.25C.0.20D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(Ⅰ)求证:![]() ∥平面
∥平面![]()
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角为300?如果存在,求出线段
所成的角为300?如果存在,求出线段![]() 的长;如果不存在,说明理由.
的长;如果不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com