设直线y=x+2与抛物线y=ax2(a>0)相交于A,B两点,M是线段AB的中点,过点M作x轴的垂线交抛物线于点N.
(Ⅰ)证明:抛物线在N点处的切线与AB平行;
(Ⅱ)是否存在实数a,使得NA⊥NB?若存在,求出a的值;若不存在,请说明理由.
【答案】
分析:(Ⅰ)将直线的方程y=x+2代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用导数的几何意义即可求得切线的斜率,从而解决问题抛物线在N点处的切线与AB平行的问题;
(Ⅱ)对于存在性问题,可先假设存在,即假设存在实数a,使得NA⊥NB,再利用M是线段AB的中点及AB的长,列出方程求出a值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(Ⅰ)由

得ax
2-x-2=0.
设A(x
1,y
1),B(x
2,y
2),则
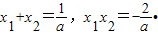
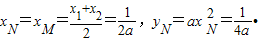
由y′=(ax
2)′=2ax知,抛物线在N点处的切线的斜率为
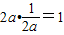
,
因此,抛物线在点N处的切线与直线AB平行.
(Ⅱ)假设存在实数a,使NA⊥NB.
由M是线段AB的中点,∴
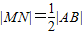
.
由MN⊥x轴,知
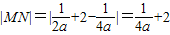
,
又
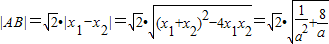
,
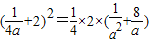
,解得
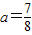
或
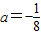
(舍去).
存在实数
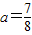
,使得NA⊥NB.
点评:此题主要考查了二次函数解析式的确定、直线与圆锥曲线的综合问题等知识;需要注意的是(2)题中存在性问题的证明方法,即对于存在性问题,可先假设存在,求出参数,若出现矛盾,则说明假设不成立,即不存在;否则存在.

 得ax2-x-2=0.
得ax2-x-2=0.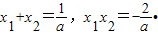
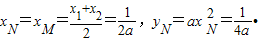
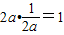 ,
,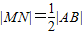 .
.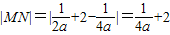 ,
,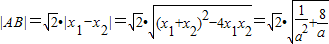 ,
,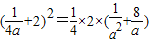 ,解得
,解得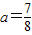 或
或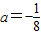 (舍去).
(舍去).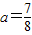 ,使得NA⊥NB.
,使得NA⊥NB.

 名校课堂系列答案
名校课堂系列答案