
【题目】已知点M(x,y)满足![]()
(1)求点M的轨迹E的方程;
(2)设过点N(﹣1,0)的直线l与曲线E交于A,B两点,若△OAB的面积为![]() (O为坐标原点).求直线l的方程.
(O为坐标原点).求直线l的方程.
科目:高中数学 来源: 题型:
【题目】在直角△ABC中,AC=![]() ,BC=1,点D是斜边AB上的动点,将△BCD沿着CD翻折至△B'CD,使得点B'在平面ACD内的射影H恰好落在线段CD上,则翻折后|AB'|的最小值是_____.
,BC=1,点D是斜边AB上的动点,将△BCD沿着CD翻折至△B'CD,使得点B'在平面ACD内的射影H恰好落在线段CD上,则翻折后|AB'|的最小值是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分![]() 分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有![]() 人.
人.
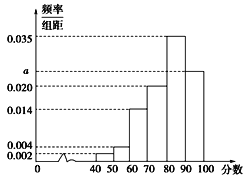
(1)求频率分布于直方图中![]() 的值,及评分等级不满意的人数;
的值,及评分等级不满意的人数;
(2)相关部门对项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)3个人坐在有八个座位的一排椅子上,若每个人的左右两边都要有空位,则不同坐法的种数为多少?
(2)某高校现有10个保送上大学的名额分配给7所高中学校,若每所高中学校至少有1个名额,则名额分配的方法共有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn,a2+a15=17,S10=55.数列{bn}满足an=log2bn.
(1)求数列{bn}的通项公式;
(2)若数列{an+bn}的前n项和Tn满足Tn=S32+18,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成60°的角;
④AB与CD所成的角是60°.
其中正确结论的序号是________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com