
已知椭圆![]() +
+![]() =1(a>b>0)的离心率为
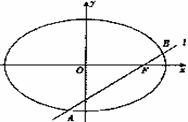
=1(a>b>0)的离心率为![]() ,右焦点为F(1,0),直线l经过点F,且与椭圆交于A、B两点,O为坐标原点.
,右焦点为F(1,0),直线l经过点F,且与椭圆交于A、B两点,O为坐标原点.
(I)求椭圆的标准方程;
(II)若P是椭圆上的一个动点,求|PO|2+|PF|2的最大值和最小值;
(III)当直线l绕点F转动时,试问:在x轴上是否存在定点S,使得![]() ?
?![]() 为常数?若存在,求出定点S的坐标;若不存在,请说明理由.
为常数?若存在,求出定点S的坐标;若不存在,请说明理由.
解:(Ⅰ)由题意可知,c=1,又e=![]() =
=![]() ,解得a=
,解得a=![]()
所以b2=a2-c2=1
所以椭圆的方程为![]() + y2=1.
+ y2=1.
(II)设P(x0,y0),则![]() ,所以2
,所以2![]() =2 -
=2 -![]() .
.
所以|PO|2+|PF|2=![]() +
+![]() +( x0-1)2+
+( x0-1)2+![]() =( x0-1)2+2
=( x0-1)2+2
因为x0∈[-![]() ,
,![]() ],所以
],所以
当x0= -![]() 时,|PO|2+|PF|2取得最大值(-
时,|PO|2+|PF|2取得最大值(-![]() -1)2+2=5+2
-1)2+2=5+2![]() ;
;
当x0= 1时,|PO|2+|PF|2取得最小值2.
(III)若直线l不垂直于x轴,可设l的方程为y=k(x-1).
由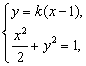
得(1+2k2)x2-4k2x+2k2-2=0.
△=16k4-4(1+2k2)(2k2-2)=8k2+8>0.
设A(x1,y1),B(x2,y2),则
x1+ x2=![]() ,x1 x2=
,x1 x2=![]() .
.
设S(t,0),则![]() =( x1-t,y1),
=( x1-t,y1),![]() =( x2-t,y2),
=( x2-t,y2),
![]() =(x1-t)(x2-t)+ y1 y2
=(x1-t)(x2-t)+ y1 y2
= x1 x2- t(x1+ x2)+ t 2+k2(x1-1)(x2-1)
=(1+ k2) x1 x2-( t +k2)( x1+ x2)+ t 2+k2
=(1+ k2)![]() -( t +k2)
-( t +k2)![]() + t 2+k2
+ t 2+k2
=![]()
=![]()
要使得![]() =λ(λ为常数),只要
=λ(λ为常数),只要![]() =λ,
=λ,
即(![]() )k2 + (t2-2 -λ)=0. (*)
)k2 + (t2-2 -λ)=0. (*)
对于任意实数k,要使(*)式恒成立,只要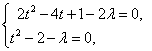
解得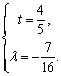
若直线l垂直于x轴,其方程为x=1.
此时,直线l与椭圆两交点为A(1,![]() )、B(1,一
)、B(1,一![]() ),
),
取点S(![]() ,0),有
,0),有![]() =(-
=(-![]() ,
,![]() ),
),![]() =(-
=(-![]() ,-
,-![]() ),
),
![]() =(-
=(-![]() )×(-
)×(-![]() )+
)+![]() ×(-
×(-![]() )
)
=![]() =λ .
=λ .
综上所述,过定点F(1,0)的动直线l与椭圆相交于A、B两点,当直线l绕点F转动时,存在定点S(![]() ,0),使得
,0),使得![]() =
=![]() .
.


科目:高中数学 来源: 题型:
A.sin30° B.cos30° C.tan30° D.sin45°
查看答案和解析>>
科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com