
【题目】已知数列![]() ,记集合
,记集合![]() .
.
(1)对于数列![]() ,写出集合
,写出集合![]() ;
;
(2)若![]() ,是否存在
,是否存在![]() ,使得
,使得![]() ?若存在,求出一组符合条件的
?若存在,求出一组符合条件的![]() ;若不存在,说明理由.
;若不存在,说明理由.
(3)若![]() ,把集合
,把集合![]() 中的元素从小到大排列,得到的新数列为
中的元素从小到大排列,得到的新数列为![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)不存在
(2)不存在![]() ,使得
,使得![]() 成立.(3)详见解析
成立.(3)详见解析
【解析】
(1)根据集合的定义![]() ,即可求解;
,即可求解;
(2)假设存在![]() ,使得
,使得![]() ,得到
,得到![]() ,根据
,根据![]() 与
与![]() 奇偶性相同,所以
奇偶性相同,所以![]() 与
与![]() 奇偶性不同,进而得到结论.
奇偶性不同,进而得到结论.
(3)若![]() ,使得
,使得![]() ,得到
,得到![]() 不成立,结合数学归纳法,把数列
不成立,结合数学归纳法,把数列![]() ,转化为数列
,转化为数列![]() ,其相应集合
,其相应集合![]() 中满足
中满足![]() 有多少项,即可得到结论.
有多少项,即可得到结论.
(1)由题意,集合![]() ,
,
可得![]() .
.
(2)假设存在![]() ,使得
,使得![]() ,
,
则有![]() ,
,
由于![]() 与
与![]() 奇偶性相同,所以
奇偶性相同,所以![]() 与
与![]() 奇偶性不同.
奇偶性不同.
又因为![]() ,
,![]() ,所以1024必有大于等于3的奇数因子,
,所以1024必有大于等于3的奇数因子,
这与1024无1以外的奇数因子矛盾.
故不存在![]() ,使得
,使得![]() 成立.
成立.
(3)首先证明![]() 时,对任意的
时,对任意的![]() 都有
都有![]() ,
,![]() .
.
若![]() ,使得:
,使得:![]() ,
,
由于![]() 与
与![]() 均大于2且奇偶性不同,所有
均大于2且奇偶性不同,所有![]() 不成立.
不成立.
其次证明除![]() 形式以外的数,都可以写成若干个连续正整数之和.
形式以外的数,都可以写成若干个连续正整数之和.
若正整数![]() ,其中
,其中![]() ,
,![]() .
.
当![]() 时,由等差数列的性质有:
时,由等差数列的性质有:
![]()
此时结论成立.
当![]() 时,由等差数列的性质有:
时,由等差数列的性质有:
![]()
![]() ,
,
此时结论成立.
对于数列![]() ,此问题等价于数列
,此问题等价于数列![]() ,其相应集合
,其相应集合![]() 中满足:
中满足:![]() 有多少项.
有多少项.
由前面的证明可知正整数2,4,8,16,32,64,128,256,512不是集合![]() 中的项,
中的项,
所以![]() 的最大值为1001.
的最大值为1001.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知某款冰淇淋的包装盒为圆台,盒盖为直径为![]() 的圆形纸片,每盒冰淇淋中包含有香草口味、巧克力口味和草莓口味冰淇淋球各一个,假定每个冰淇淋球都是半径为
的圆形纸片,每盒冰淇淋中包含有香草口味、巧克力口味和草莓口味冰淇淋球各一个,假定每个冰淇淋球都是半径为![]() 的球体,三个冰淇淋球两两相切,且都与冰淇淋盒盖、盒底和盒子侧面的曲面相切,则冰淇淋盒的体积为______.
的球体,三个冰淇淋球两两相切,且都与冰淇淋盒盖、盒底和盒子侧面的曲面相切,则冰淇淋盒的体积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,沿河有A、B两城镇,它们相距![]() 千米.以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放.两城镇可以单独建污水处理厂,或者联合建污水处理厂(在两城镇之间或其中一城镇建厂,用管道将污水从各城镇向污水处理厂输送).依据经验公式,建厂的费用为
千米.以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放.两城镇可以单独建污水处理厂,或者联合建污水处理厂(在两城镇之间或其中一城镇建厂,用管道将污水从各城镇向污水处理厂输送).依据经验公式,建厂的费用为![]() (万元),
(万元),![]() 表示污水流量;铺设管道的费用(包括管道费)
表示污水流量;铺设管道的费用(包括管道费)![]() (万元),
(万元),![]() 表示输送污水管道的长度(千米).已知城镇A和城镇B的污水流量分别为
表示输送污水管道的长度(千米).已知城镇A和城镇B的污水流量分别为![]() 、
、![]() ,
,![]() 、
、![]() 两城镇连接污水处理厂的管道总长为
两城镇连接污水处理厂的管道总长为![]() 千米.假定:经管道输送的污水流量不发生改变,污水经处理后直接排入河中.请解答下列问题(结果精确到
千米.假定:经管道输送的污水流量不发生改变,污水经处理后直接排入河中.请解答下列问题(结果精确到![]() ):
):
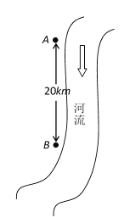
(1)若在城镇A和城镇B单独建厂,共需多少总费用?
(2)考虑联合建厂可能节约总投资,设城镇A到拟建厂的距离为![]() 千米,求联合建厂的总费用
千米,求联合建厂的总费用![]() 与
与![]() 的函数关系式,并求
的函数关系式,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用平面截圆柱面,当圆柱的轴与![]() 所成角为锐角时,圆柱面的截面是一个椭圆,著名数学家
所成角为锐角时,圆柱面的截面是一个椭圆,著名数学家![]() 创立的双球实验证明了上述结论.如图所示,将两个大小相同的球嵌入圆柱内,使它们分别位于
创立的双球实验证明了上述结论.如图所示,将两个大小相同的球嵌入圆柱内,使它们分别位于![]() 的上方和下方,并且与圆柱面和
的上方和下方,并且与圆柱面和![]() 均相切.给出下列三个结论:
均相切.给出下列三个结论:
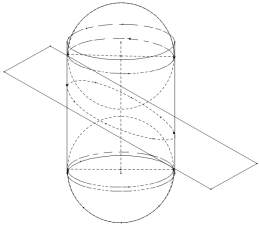
①两个球与![]() 的切点是所得椭圆的两个焦点;
的切点是所得椭圆的两个焦点;
②若球心距![]() ,球的半径为
,球的半径为![]() ,则所得椭圆的焦距为2;
,则所得椭圆的焦距为2;
③当圆柱的轴与![]() 所成的角由小变大时,所得椭圆的离心率也由小变大.
所成的角由小变大时,所得椭圆的离心率也由小变大.
其中,所有正确结论的序号是( )
A.①B.②③C.①②D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我们的教材必修一中有这样一个问题,假设你有一笔资金,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报![]() 元;
元;
方案二:第一天回报![]() 元,以后每天比前一天多回报
元,以后每天比前一天多回报![]() 元;
元;
方案三:第一天回报![]() 元,以后每天的回报比前一天翻一番.
元,以后每天的回报比前一天翻一番.
记三种方案第![]() 天的回报分别为
天的回报分别为![]() ,
,![]() ,
,![]() .
.
(1)根据数列的定义判断数列![]() ,
,![]() ,
,![]() 的类型,并据此写出三个数列的通项公式;
的类型,并据此写出三个数列的通项公式;
(2)小王准备做一个为期十天的短期投资,他应该选择哪一种投资方案?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且AB=1,BC=2, ∠ABC=60°,PA⊥平面ABCD,AE⊥PC于E,
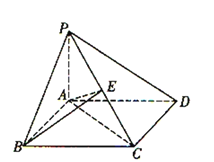
下列四个结论:①AB⊥AC;②AB⊥平面PAC;③PC⊥平面ABE;④BE⊥PC.正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=6sinθ,建立以极点为坐标原点,极轴为x轴正半轴的平面直角坐标系.直线l的参数方程是![]() ,(t为参数).
,(t为参数).
(1)求曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点,且|AB|=![]() ,求直线的斜率k.
,求直线的斜率k.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com