
【题目】某投资人欲将5百万元资金投人甲、乙两种理财产品,根据银行预测,甲、乙两种理财产品的收益与投入资金的关系式分别为![]() ,
,![]() ,其中
,其中![]() 为常数且
为常数且![]() .设对乙种产品投入资金
.设对乙种产品投入资金![]() 百万元.
百万元.
(Ⅰ)当![]() 时,如何进行投资才能使得总收益
时,如何进行投资才能使得总收益![]() 最大;(总收益
最大;(总收益![]() )
)
(Ⅱ)银行为了吸储,考虑到投资人的收益,无论投资人资金如何分配,要使得总收益不低于0.45百万元,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)甲种产品投资4百万元,乙种产品投资1百万元时,总收益最大(Ⅱ)
【解析】
(Ⅰ)当![]() 时求出总收益
时求出总收益![]() 的解析式,结合一元二次函数最值性质进行求解即可.
的解析式,结合一元二次函数最值性质进行求解即可.
(Ⅱ)根据题意可知![]() 对任意
对任意![]() 恒成立,将问题转化为即
恒成立,将问题转化为即![]() 对任意
对任意![]() 恒成立,再利用换元法转化为一元二次不等式恒成立求解.
恒成立,再利用换元法转化为一元二次不等式恒成立求解.
(Ⅰ)设对乙种产品投入资金![]() 百万元,则对甲种产品投入资金
百万元,则对甲种产品投入资金![]() 百万元
百万元
当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]() ,
,
![]() ,其图象的对称轴
,其图象的对称轴![]() ,
,
∴当![]() 时,总收益
时,总收益![]() 有最大值,此时
有最大值,此时![]() ,
,![]() .
.
即甲种产品投资4百万元,乙种产品投资1百万元时,总收益最大
(Ⅱ)由题意知![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,
,
设![]() ,则
,则![]() ,
,
则![]() ,其图象的对称轴为
,其图象的对称轴为![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
且![]() ,
,
∴![]() ,得
,得![]() ,又
,又![]() ,
,
∴![]() ,
,
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
且![]() ,可得
,可得![]() ,符合题意,
,符合题意,
∴![]()
③当![]() ,即
,即![]() 时,易知
时,易知![]() 在
在![]() 单调递增,
单调递增,
可得![]() 恒成立,
恒成立,![]() ,
,
综上可得![]() .
.
∴实数![]() 的取值范围是
的取值范围是 .
.


科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() 且函数
且函数![]() ,若函数f(x)的图象上两个相邻的对称轴距离为
,若函数f(x)的图象上两个相邻的对称轴距离为![]() .
.
(1)求函数f(x)的解析式;
(2)将函数y=f(x)的图象向左平移![]() 个单位后,得到函数y=g(x)的图象,求函数g(x)的表达式并其对称轴;
个单位后,得到函数y=g(x)的图象,求函数g(x)的表达式并其对称轴;
(3)若方程f(x)=m(m>0)在![]() 时,有两个不同实数根x1,x2,求实数m的取值范围,并求出x1+x2的值.
时,有两个不同实数根x1,x2,求实数m的取值范围,并求出x1+x2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学导师计划从自己所培养的研究生甲、乙两人中选一人,参加雄安新区某部门组织的计算机技能大赛,两人以往5次的比赛成绩统计如下:(满分100分,单位:分).
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩 | 87 | 87 | 84 | 100 | 92 |
乙的成绩 | 100 | 80 | 85 | 95 | 90 |
(1)试比较甲、乙二人谁的成绩更稳定;
(2)在一次考试中若两人成绩之差的绝对值不大于2,则称两人“实力相当”.若从上述5次成绩中任意抽取2次,求恰有一次两人“实力相当”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在个矩形ABCD的池底水平铺设污水净化管道(![]() ,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且
,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且![]() ,
,![]() ,设
,设![]() .
.
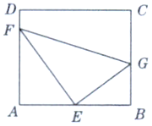
(1)试将污水管道的长度l表示成![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 为何值时,污水净化效果最好,并求此时管道的长度.
为何值时,污水净化效果最好,并求此时管道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为其右焦点,
为其右焦点, ![]() 是椭圆的左、右顶点,点
是椭圆的左、右顶点,点![]() 满足
满足![]() .
.
①证明: ![]() 为定值;
为定值;
②设![]() 是直线
是直线![]() 上的任一点,直线
上的任一点,直线![]() 分别另交椭圆
分别另交椭圆![]() 于
于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和椭圆
和椭圆![]() ,
, ![]() 是椭圆
是椭圆![]() 的左焦点.
的左焦点.
(Ⅰ)求椭圆![]() 的离心率和点
的离心率和点![]() 的坐标;
的坐标;
(Ⅱ)点![]() 在椭圆
在椭圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,交圆
轴的垂线,交圆![]() 于点
于点![]() (
(![]() 不重合),
不重合),![]() 是过点
是过点![]() 的圆
的圆![]() 的切线.圆
的切线.圆![]() 的圆心为点
的圆心为点![]() ,半径长为
,半径长为![]() .试判断直线
.试判断直线![]() 与圆
与圆![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法的错误的是( )
A. 经过定点![]() 的倾斜角不为
的倾斜角不为![]() 的直线的方程都可以表示为
的直线的方程都可以表示为![]()
B. 经过定点![]() 的倾斜角不为
的倾斜角不为![]() 的直线的方程都可以表示为
的直线的方程都可以表示为![]()
C. 不经过原点的直线的方程都可以表示为![]()
D. 经过任意两个不同的点![]() 、
、![]() 直线的方程都可以表示为
直线的方程都可以表示为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com