练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数，.

    （1）当时，求的值域；

    （2）当时，不等式恒成立（是的导函数），求实数的取值范围.

    【答案】（1）；（2）

    【解析】

    （1）求导，令，求出极值点，利用导数求出函数的单调性，即可得出内的最值，即可得出值域；

    （2）根据题意，构造新函数，将不等式的恒成立问题，转化为在内的恒成立问题，求导，再二次求导，通过单调性求出最值，即可求出参数的取值范围.

    （1）由题可得.

    令，得.

    当时，，当时，，

    所以，

    .

    因为，所以，

    所以的值域为.

    （2）由得，

    即.

    设，则.

    设，则.

    当时，，，所以.

    所以即在上单调递增，则.

    若，则，所以在上单调递增.

    所以恒成立，符合题意.

    若，则，必存在正实数，

    满足：当时，，单调递减，此时，不符合题意.

    综上所述，的取值范围是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，直线的参数方程为（为参数，为直线的倾斜角），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

    （1）写出曲线的直角坐标方程，并求时直线的普通方程；

    （2）直线和曲线交于两点，点的直角坐标为，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，曲线在点处的切线方程为。

    （1）求、的值；

    （2）如果当，且时， ，求的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，有一块半圆形空地，开发商计划建造一个矩形游泳池及左右两侧两个大小相同的矩形休息区，其中半圆的圆心为，半径为，矩形的一边在上，矩形的一边在上，点在圆周上，在直径上，且，设．若每平方米游泳池的造价与休息区造价之比为.

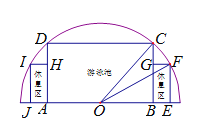
    （1）记游泳池及休息区的总造价为，求的表达式；

    （2）为进行投资预算，当为何值时，总造价最大？并求出总造价的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4—5：不等式选讲]

    已知函数．

    （1）当时，求不等式的解集；

    （2）若不等式的解集包含，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD相交于点O，EF∥AB，EFAB，平面BCF⊥平面ABCD，BF＝CF，G为BC的中点，求证：

    （1）OG∥平面ABFE；

    （2）AC⊥平面BDE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：x∈[1，2]，log2（x+2）＜2m；命题q：关于x的方程x2﹣x+m2＝0有两个不同的实数根.

    （1）若（￢p）∧q为真命题，求实数m的取值范围；

    （2）若p∨q为真命题，p∧q为假命题，求实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为，点是抛物线上一点，且满足.

    （1）求、的值；

    （2）设、是抛物线上不与重合的两个动点，记直线、与的准线的交点分别为、，若，问直线是否过定点？若是，则求出该定点坐标，否则请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的多面体ABCDEF满足：正方形ABCD与正三角形FBC所在的两个平面互相垂直，FB∥AE且FB＝2EA.

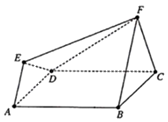
    （1）证明：平面EFD⊥平面ABFE；

    （2）求二面角E﹣FD﹣C的余弦值.

    查看答案和解析>>

    同步练习册答案