Question

如下图示，正三棱台的上、下底面边长分别为3 cm和6 cm，高是cm．求：

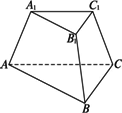
(1)三棱台的侧棱长；

(2)斜高；

(3)侧棱与底面所成的角的正切值；

(4)侧面与底面所成的角；

(5)侧面积．

Answer 1

答案：
解析：

设O1、O分别是上、下底面中心，则O1O＝cm． 　　连结A1O1，并延长交B1C1于点D1；连结AO，并延长交BC于点D． 　　过A1作A1F⊥AD于点F，作D1E⊥AD于点E． 　　(1)在Rt△A1AF中，A1F＝cm，AF＝AO－A1O1＝(6－3)＝(cm)， 　　∴AA1＝(cm)． 　　(2)在Rt△D1DE中，D1E＝，DE＝DO－D1O1＝(6－3)＝(cm)， 　　∴斜边上的高D1D＝(cm)． 　　(3)∵A1F⊥底面ABC， 　　∴∠A1AF为侧棱与底面所成的角． 　　∴tan∠A1AF＝． 　　(4)方法一：∵D1D⊥BC，AD⊥BC， 　　∴∠D1DA为侧面与底面所成二面角的平面角． 　　∴tan∠D1DA＝．∴∠D1DA＝60°． 　　方法二：(还台为锥)设棱锥的高为h，利用OA＝2OD， 　　得tan∠D1DE＝＝2tan∠A1AF＝． 　　(5)方法一：S侧＝(3×3＋3×6)×＝(cm2)． 　　方法二：S侧＝＝2(S下－S上)＝2×(62－32)＝(cm2)． 　　思路分析：利用图中的直角三角形与直角梯形进行求解．

提示：

正棱锥、正棱台的问题可转化为直角三角形问题，使高、斜高、斜高在底面上的射影，侧棱、侧棱在底面上的射影，底面边长之半，边心距，外接圆半径及侧棱和底面所成的角，侧面和底面所成的二面角等元素转化为直角三角形的边和角． 　　“还台体为锥体”有利于整体上把握本章内容和公式．对正棱锥、正棱台，若侧面与底面所成角为α，则可利用公式S正棱锥侧＝，S正棱台侧＝．