
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 是菱形,其对角线的交点为
是菱形,其对角线的交点为![]() ,且
,且![]() ,
,![]() .
.
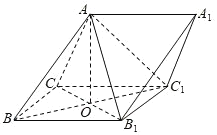
(1)求证:![]() 平面
平面![]() ;
;
(2)设![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】自2017年7月27日上映以来,《战狼2》的票房一路高歌猛进,并不断刷新华语电影票房纪录.继8月25日官方宣布冲破53亿票房之后,根据外媒Worldwide Box Office给出的2017年周末全球票房最新排名,《战狼2》以8.151亿美元(约54.18亿元)的成绩成功杀入前五.通过收集并整理了《战狼2》上映前两周的票房(单位:亿元)数据,绘制出下面的条形图.根据该条形图,下列结论错误的是( )
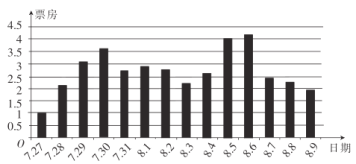
A.在《战狼2》上映前两周中,前四天票房逐日递增
B.在《战狼2》上映前两周中,日票房超过2亿元的共有12天
C.在《战狼2》上映前两周中,8月5日,8月6日达到了票房的高峰期
D.在《战狼2》上映前两周中,前五日的票房平均数高于后五日的票房平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建设美丽新农村,某村对本村布局重新进行了规划,其平面规划图如图所示,其中平行四边形![]() 区域为生活区,
区域为生活区,![]() 为横穿村庄的一条道路,
为横穿村庄的一条道路,![]() 区域为休闲公园,
区域为休闲公园,![]() ,
,![]() ,
,![]() 的外接圆直径为
的外接圆直径为![]() .
.

(1)求道路![]() 的长;
的长;
(2)该村准备沿休闲公园的边界修建栅栏,以防村中的家畜破坏公园中的绿化,试求栅栏总长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]()
(1)求![]() 的轨迹
的轨迹![]()
(2)过轨迹![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() ,设直线
,设直线![]() 的斜率分别是
的斜率分别是![]() ,试问在三个斜率都存在且不为0的条件下,
,试问在三个斜率都存在且不为0的条件下, 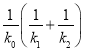 是否是定值,请说明理由,并加以证明.
是否是定值,请说明理由,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n为正整数,称n×n的方格表Tn的网格线的交点(共(n+1)2个交点)为格点.现将数1,2,……,(n+1)2分配给Tn的所有格点,使不同的格点分到不同的数.称Tn的一个1×1格子S为“好方格”,如果从2S的某个顶点起按逆时针方向读出的4个顶点上的数依次递增(如图是将数1,2,…,9分配给T2的格点的一种方式,其中B、C是好方格,而A、D不是好方格)设Tn中好方格个数的最大值为f(n).
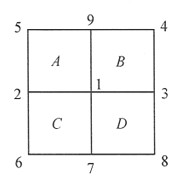
(1)求f(2)的值;
(2)求f(n)关于正整数n的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列结论正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.
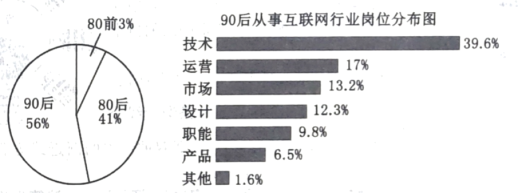
A.互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时参加一次数学测试,共有20道选择题,每题均有4个选项,答对得3分,答错或不答得0分,甲和乙都解答了所有的试题,经比较,他们只有2道题的选项不同,如果甲最终的得分为54分,那么乙的所有可能的得分值组成的集合为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (
(![]() ,
,![]() )的部分图象如图中实线所示,图中圆C与
)的部分图象如图中实线所示,图中圆C与![]() 的图象交于M,N两点,且M在y轴上,则下列说法中正确的是( )
的图象交于M,N两点,且M在y轴上,则下列说法中正确的是( )

A.函数![]() 的最小正周期是2π
的最小正周期是2π
B.函数![]() 的图象关于点
的图象关于点![]() 成中心对称
成中心对称
C.函数![]() 在
在![]() 单调递增
单调递增
D.将函数![]() 的图象向左平移
的图象向左平移![]() 后得到的关于y轴对称
后得到的关于y轴对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com