记定义在[-1,1]上的函数f(x)=x2+px+q(p,q∈R)的最大值与最小值分别为M,m.又记h(p)=M-m.
(Ⅰ)当0≤p≤2时,求M、m(用p,q表示),并证明h(p)≥1;
(Ⅱ)写出h(p)的解析式(不必写出求解过程);
(Ⅲ)在所有形如题设的函数f(x)中,求出这样的f(x),使得|f(x)|的最大值为最小.
【答案】
分析:(Ⅰ)根据每件
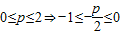
,又f(x)图象开口向上,得出最大值与最小值,从而求得h(p)并证明h(p)≥1;
(Ⅱ)对字母p进行分类讨论后写出出h(p)的解析式即可;
(Ⅲ)由(Ⅱ)知h(p)的解析式,结合M-m≥1及取得最值的条件得出,p=0,M=1+q,m=q.最后结合由M=-m得1+q=-q求得q,最后写出所求函数式即可.
解答:解:(Ⅰ)
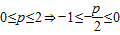
,又f(x)图象开口向上,
∴
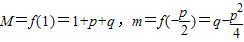
∴
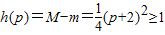
(4分)
(Ⅱ)
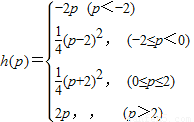
(Ⅲ)由(Ⅱ)知

,∴M-m≥1.
∵在[-1,1]上,总有
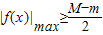
,当且仅当M=-m时取”=”;
又,
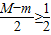
,当且仅当p=0时取“=”,
∴当
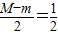
时的f(x)符合条件.
此时,p=0,M=1+q,m=q.由M=-m得1+q=-q.∴
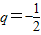
即所求函数为:f(x)=
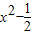
.(13分)
点评:本小题主要考查函数解析式的求解及常用方法、函数的最值及其几何意义等基础知识,考查运算求解能力与转化思想.属于基础题.

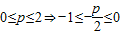 ,又f(x)图象开口向上,得出最大值与最小值,从而求得h(p)并证明h(p)≥1;
,又f(x)图象开口向上,得出最大值与最小值,从而求得h(p)并证明h(p)≥1;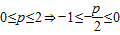 ,又f(x)图象开口向上,
,又f(x)图象开口向上,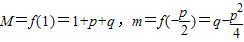
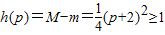 (4分)
(4分)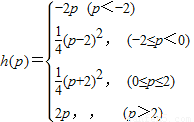
 ,∴M-m≥1.
,∴M-m≥1.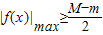 ,当且仅当M=-m时取”=”;
,当且仅当M=-m时取”=”;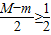 ,当且仅当p=0时取“=”,
,当且仅当p=0时取“=”,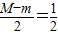 时的f(x)符合条件.
时的f(x)符合条件.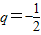
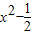 .(13分)
.(13分)

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案