练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．若|z|=1，则|z+$\frac{1}{z}$|的取值范围[0，2]．

    分析 设z=a+bi，则a2+b2=1，且-1≤a≤1．由此推导出z+$\frac{1}{z}$=2a，由此能求出|z+$\frac{1}{z}$|的取值范围．

    解答 解：设z=a+bi，则a2+b2=1，且-1≤a≤1．
    ∴z+$\frac{1}{z}$=a+bi+$\frac{1}{a+bi}$=a+bi+$\frac{a-bi}{{a}^{2}+{b}^{2}}$=a+bi+a-bi=2a，
    ∴|z+$\frac{1}{z}$|=|2a|∈[0，2]．
    ∴|z+$\frac{1}{z}$|的取值范围是[0，2]．

    点评 本题考查复数模的取值范围的求法，是基础题，注意复数的代数形式的乘除运算法则的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．已知双曲线$\frac{{x}^{2}}{a^2}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F（4，0），若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点，则a的取值范围是0＜a≤2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

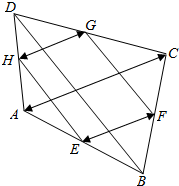    4．如图，E，F，G，H分别是四边形ABCD的各边中点，分别指出图中：
    （1）与向量$\overrightarrow{HG}$相等的向量；
    （2）与向量$\overrightarrow{HG}$平行的向量；
    （3）与向量$\overrightarrow{HG}$模相等的向量；
    （4）与向量$\overrightarrow{HG}$模相等、方向相反的向量．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．计算下列不定积分
    （1）∫$\frac{{3}^{x}-{e}^{x}}{{2}^{x}}$dx；
    （2）∫$\frac{1}{{x}^{2}（1+{x}^{2}）}$dx．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．以原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=6cosθ，在平面直角坐标系xOy中，直线l经过点P（3，4），斜率为1．
    （1）求曲线C的直角坐标方程；
    （2）设直线l与圆C相交于A，B两点，求|PA|•|PB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．方程x3-3x+c=0在[0，1]上只有一个实数根，求c的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=$\frac{1}{2}$x-$\frac{1}{4}$sinx-$\frac{\sqrt{3}}{4}$cosx的图象在点A（x0，f（x0））处的切线斜率为$\frac{1}{2}$，求tanx0的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．下列三个图分别是四棱锥A-BCEF的直观图、侧视图、俯视图，在直观图中，侧面ABC⊥底面BCEF，M为AC的中点，侧视图是等边三角形，俯视图是直角梯形，有关数据如图所示．
    （1）求证：BM∥面AEF；
    （2）求证：AE⊥BM；
    （3）求该四棱锥A-BCEF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．某人在早晨6时至7时的某时刻开始晨练，7时至8时的某时刻结束晨练，结果发现晨练结束时与晨练开始时，手表的时针与分针恰好交换位置，这个人共晨练$\frac{720}{13}$分钟．

    查看答案和解析>>

    同步练习册答案