
���� ��5������ֱ�����жϣ����ɵó����ۣ�
��� �⣺�������εİ뾶Ϊ1���ܳ�Ϊ4������Ϊ2��������ε�Բ�ĽǵĻ������ľ���ֵΪ2����ȷ��
�ں���f��x��=$\frac{2x-1}{x-1}$=2+$\frac{1}{x-1}$��ͼ��ĶԳ������ǵ㣨1��2������ȷ��
����֪$\overrightarrow{a}$=��2��1����$\overrightarrow{b}$=��1��1������$\overrightarrow{a}$��$\overrightarrow{b}$�����ϵ�ͶӰΪ$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{3}{\sqrt{2}}$������ȷ��
��������x2+��a+2��x+a=0��һ����ʵ����һ����ʵ������a��0����ȷ��
�ݸ��ݺ���y=|1-x2|��ͼ��֪������y=|1-x2|��ֱ��y=m����m��R���Ĺ����������������1������ȷ��
�ʴ�Ϊ���٢ڢܣ�
���� �����Ǹ��е��⣮���麯��ͼ��ĶԳƱ仯��һԪ���η��̸������⣬�Լ����ε�Բ�ĽǵĻ��ȵȻ���֪ʶ������ѧ�����Ӧ��֪ʶ������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
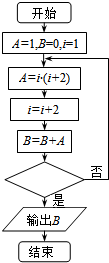 ��ͼ�������Ǽ���1��3+3��5+5��7+��+13��15��ֵ��һ�������ͼ�������жϿ���Ӧ�������������ȷ���ǣ�������
��ͼ�������Ǽ���1��3+3��5+5��7+��+13��15��ֵ��һ�������ͼ�������жϿ���Ӧ�������������ȷ���ǣ�������| A�� | i��13�� | B�� | i��14�� | C�� | i��14�� | D�� | i��15�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com