
【题目】已知{an}是等差数列,其前n项和为Sn , {bn}是等比数列,且a1=b1=2,a4+b4=27,S4﹣b4=10.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=anb1+an﹣1b2+…+a1bn , n∈N* , 是否存在实数p,q,r,对于任意n∈N* , 都有Tn=pan+qbn+r,若存在求出p,q,r的值,若不存在说明理由.
【答案】
(1)解:设等差数列的公差为d,等比数列的公比为q,
由a1=b1=2,得a4=2+3d,b4=2q3,s4=8+6d,
由a4+b4=27,S4﹣b4=10得, ![]() ,
,
解得d=3,q=2,
所以an=3n﹣1,bn=2n
(2)解:假设存在实数p,q,r,对于任意n∈N*,都有Tn=pan+qbn+r,
由(1)得,Tn=anb1+an﹣1b2+…+a1bn
= ![]() ①
①
∴2Tn= ![]() ②
②
由②﹣①得,
Tn=﹣2(3n﹣1)+3×(22+23+…+2n)+2n+2
=3× ![]() +2n+2﹣6n+2
+2n+2﹣6n+2
=102n﹣6n﹣10
∴Tn=﹣2(3n﹣1)+10×2n﹣12=pan+qbn+r,
可得p=﹣2;q=10;r=﹣12,
即存在p=﹣2;q=10;r=﹣12满足条件
【解析】(1)设出首项和公差,根据等差、等比数列的通项公式和等差数列的前n项和公式,列出方程组求出首项和公差,即可求出an、bn;(2)假设存在实数p、q、r满足条件,由(1)表示出Tn , 利用错位相减法求出Tn的表达式化简后即可求出实数p、q、r的值.
【考点精析】认真审题,首先需要了解等差数列的通项公式(及其变式)(通项公式:![]() 或
或![]() ),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系
),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系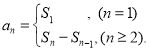 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: 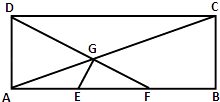
(1)若动点M到D点距离等于它到C点距离的两倍,求动点M的轨迹围成区域的面积;
(2)证明:E G⊥D F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个乒乓球协会的分别选派3,1,2名运动员参加某次比赛,甲协会运动员编号分别为A1 , A2 , A3 , 乙协会编号为A4 , 丙协会编号分别为A5 , A6 , 若从这6名运动员中随机抽取2名参加双打比赛.
(1)用所给编号列出所有可能抽取的结果;
(2)求丙协会至少有一名运动员参加双打比赛的概率;
(3)求参加双打比赛的两名运动员来自同一协会的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若函数
时,若函数![]() 的导函数
的导函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,其横坐标分别为
两点,其横坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,且
,且![]() ,
, ![]() 恰为函数
恰为函数![]() 的零点,求证:
的零点,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)= ![]() ,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是 .
,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′= ![]() ,连接CC′,E为CC′的中点.
,连接CC′,E为CC′的中点. 
文科:
(1)求证:AC′∥平面BDE;
(2)求证:CC′⊥平面BDE;
(3)求三棱锥C′﹣BCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com