
【题目】已知圆![]() ,圆
,圆![]() 与
与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的圆的切线为
的圆的切线为![]() 是圆上异于
是圆上异于![]() 的一点,
的一点,![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 是
是![]() 的中点,延长
的中点,延长![]() 分别交
分别交![]() 于
于![]() .
.

(1)若点![]() ,求以
,求以![]() 为直径的圆的方程,并判断
为直径的圆的方程,并判断![]() 是否在圆上;
是否在圆上;
(2)当![]() 在圆上运动时,证明:直线
在圆上运动时,证明:直线![]() 恒与圆
恒与圆![]() 相切.
相切.
【答案】(1)圆的方程为![]() ,且
,且![]() 在圆上;(2)证明见解析.
在圆上;(2)证明见解析.
【解析】试题分析:(1)已知点![]() 、
、![]() 的坐标,可求出直线
的坐标,可求出直线![]() 的方程,可求出点
的方程,可求出点![]() 的坐标,由圆的方程可知点
的坐标,由圆的方程可知点![]() 的坐标,可求出以
的坐标,可求出以![]() 为直径的圆的方程,将点
为直径的圆的方程,将点![]() 的坐标代入圆的方程,得在圆上;(2)要证明结论,需证明
的坐标代入圆的方程,得在圆上;(2)要证明结论,需证明![]() ,可先设点
,可先设点![]() 坐标,可求点
坐标,可求点![]() 坐标,进而可求点
坐标,进而可求点![]() 坐标,得
坐标,得![]() 与
与![]() 斜率,得
斜率,得![]() 得结论.
得结论.
试题解析:(1)由![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,由
,由![]() ,
,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,∴
,∴![]() 为线段
为线段![]() 的中点,以
的中点,以![]() 为直径的圆恰以
为直径的圆恰以![]() 为圆心,半径等于
为圆心,半径等于![]() ,
,
所以,所求圆的方程为![]() ,且
,且![]() 在圆上,
在圆上,
(2)设![]() ,则
,则![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
在此方程中令![]() ,得
,得![]() ,
,
直线![]() 的斜率
的斜率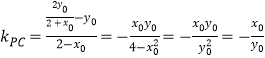 ,
,
若![]() ,则此时
,则此时![]() 与
与![]() 轴垂直,即
轴垂直,即![]() ,若
,若![]() ,则此时直线
,则此时直线![]() 的斜率为
的斜率为![]()
∴![]() ,即
,即![]() ,则直线
,则直线![]() 与圆
与圆![]() 相切
相切


科目:高中数学 来源: 题型:
【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响.部分统计数据如下表:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
合计 | 20 | 10 | 30 |
附表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
经计算![]() ,则下列选项正确的是( )
,则下列选项正确的是( )
A.有99.5%的把握认为使用智能手机对学习有影响
B.有99.5%的把握认为使用智能手机对学习无影响
C.有99.9%的把握认为使用智能手机对学习有影响
D.有99.9%的把握认为使用智能手机对学习无影响
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求![]() 的展开式中
的展开式中![]() 的系数及展开式中各项系数之和;
的系数及展开式中各项系数之和;
(2)从0,2,3,4,5,6这6个数字中任取4个组成一个无重复数字的四位数,求满足条件的四位数的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱![]() 中,
中,![]() 为正方形,
为正方形,![]() 为菱形,
为菱形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(1)求证:![]() ;
;
(2)设点![]() 、
、![]() 分别是
分别是![]() ,
,![]() 的中点,试判断直线
的中点,试判断直线![]() 与平面
与平面![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某件商品的经验表明,该商品每日的销量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足关系式
(单位:元/千克)满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若该商品的成本为3元/千克,试确定销售价格![]() 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。
查看答案和解析>>
科目:高中数学 来源: 题型:
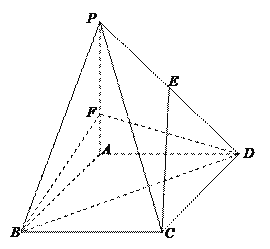
【题目】如图,在边长为3的菱形ABCD中,∠ABC=60°,![]() 平面ABCD,且
平面ABCD,且![]() ,E为PD中点,F在棱PA上,且
,E为PD中点,F在棱PA上,且![]() .
.
(1)求证:CE∥平面BDF;
(2)求点P到平面BDF的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
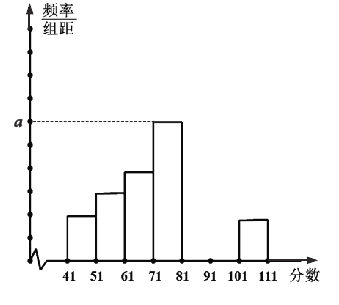
【题目】下面是某市环保局连续30天对空气质量指数的监测数据:
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
(Ⅰ)完成下面的频率分布表;
(Ⅱ)完成下面的频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;
(Ⅲ)在本月空气质量指数大于等于91的这些天中随机选取两天,求这两天中至少有一天空气质量指数在区间![]() 内的概率.
内的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com