
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C上横坐标为3的点M到焦点F的距离为4.
(1)求抛物线C的方程;
(2)过抛物线C的焦点F且斜率为1的直线l交抛物线C于A、B两点,求弦长|AB|.
【答案】(1)y2=4x;(2)8.
【解析】
(1)求得抛物线的焦点和准线方程,运用抛物线的定义可得p的方程,求得p,即可得到所求抛物线方程;
(2)求得直线l的方程为y=x-1,设A(x1,y1),B(x2,y2),联立抛物线方程,消去y,可得x的方程,运用韦达定理和弦长公式,计算可得所求值.
解:(1)抛物线C:y2=2px(p>0)的焦点F(![]() ,0),准线方程为x=-
,0),准线方程为x=-![]() ,
,
∵|MF|=4,由抛物线的定义可得![]() ,
,
∴p=2.故所求抛物线方程为y2=4x;
(2)由(1)得p=2,焦点F(1,0),所以直线l的方程为y=x-1,
并设A(x1,y1),B(x2,y2),
联立![]() ,消去y,得x2-6x+1=0,
,消去y,得x2-6x+1=0,
所以x1+x2=6,
可得x1+x2+p=8,
所以|AB|=8.


科目:高中数学 来源: 题型:
【题目】如图,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿直线
沿直线![]() 折起到
折起到![]() 的位置(点
的位置(点![]() 不与
不与![]() ,
,![]() 两点重合).
两点重合).

(1)求证:不论![]() 折起到何位置,都有
折起到何位置,都有![]() 平面
平面![]() ;
;
(2)当![]() 平面
平面![]() 时,点
时,点![]() 是线段
是线段![]() 上的一个动点,若
上的一个动点,若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学参加一项射击游戏,两人约定,其中任何一人每射击一次,击中目标得2分,未击中目标得0分.若甲、乙两名同学射击的命中率分别为![]() 和p,且甲、乙两人各射击一次所得分数之和为2的概率为
和p,且甲、乙两人各射击一次所得分数之和为2的概率为![]() ,假设甲、乙两人射击互不影响.
,假设甲、乙两人射击互不影响.
(1)求p的值;
(2)记甲、乙两人各射击一次所得分数之和为X,求X的分布列和均值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,命题
,命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆,命题
轴上的椭圆,命题![]() 方程
方程![]() 表示双曲线.
表示双曲线.
(1)若命题![]() 是真命题,求实数
是真命题,求实数![]() 的范围;
的范围;
(2)若命题“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”是假命题,求实数
”是假命题,求实数![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|1-a≤x≤1+a}(a>0),B={x|x2-5x+4≤0}.
(1)若“x∈A”是“x∈B”的必要不充分条件,求实数a的取值范围;
(2)对任意x∈B,不等式x2-mx+4≥0都成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的面积为
的面积为![]() ,且与
,且与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点.
两点.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与线段
与线段![]() 相交,求实数
相交,求实数![]() 的取值范围;
的取值范围;
(3)试讨论直线![]() 与(1)小题所求圆
与(1)小题所求圆![]() 的交点个数.
的交点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}中,a2=-8,a6=0.
(1)求数列{an}的通项公式;
(2)若等比数列{bn}满足b1=-8,b2=a1+a2+a3,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现代城市大多是棋盘式布局(如北京道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义![]() ,
,![]() 两点间的“直角距离”为:
两点间的“直角距离”为:![]() .
.
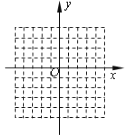
(1)在平面直角坐标系中,写出所有满足到原点的“直角距离”为2的“格点”的坐标.(格点指横、纵坐标均为整数的点)
(2)求到两定点![]() 、
、![]() 的“直角距离”和为定值
的“直角距离”和为定值![]() 的动点轨迹方程,并在直角坐标系内作出该动点的轨迹.(在以下三个条件中任选一个做答)
的动点轨迹方程,并在直角坐标系内作出该动点的轨迹.(在以下三个条件中任选一个做答)
①![]() ,
,![]() ,
,![]() ;
;
②![]() ,
,![]() ,
,![]() ;
;
③![]() ,
,![]() ,
,![]() .
.
(3)写出同时满足以下两个条件的“格点”的坐标,并说明理由(格点指横、纵坐标均为整数的点).
①到![]() ,
,![]() 两点“直角距离”相等;
两点“直角距离”相等;
②到![]() ,
,![]() 两点“直角距离”和最小.
两点“直角距离”和最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量![]() (单位:
(单位:![]() )和与它“相近”的株数
)和与它“相近”的株数![]() 具有线性相关关系(两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出该种水果每株的产量![]() 关于它“相近”株数
关于它“相近”株数![]() 的回归方程;
的回归方程;
(2)有一种植户准备种植该种水果500株,且每株与它“相近”的株数都为![]() ,计划收获后能全部售出,价格为10元
,计划收获后能全部售出,价格为10元![]() ,如果收入(收入=产量×价格)不低于25000元,则
,如果收入(收入=产量×价格)不低于25000元,则![]() 的最大值是多少?
的最大值是多少?
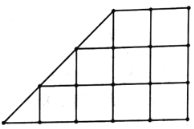
(3)该种植基地在如图所示的直角梯形地块的每个交叉点(直线的交点)处都种了一株该种水果,其中每个小正方形的边长和直角三角形的直角边长都为![]() ,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: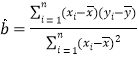 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com