
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点,△AEC面积的最小值是3.

(1)求证:AC⊥DE;
(2)求四棱锥P-ABCD的体积.
(1)详见解析,(2)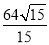 .
.
【解析】
试题分析:(1)证明线线垂直,一般利用线面垂直性质与判定定理进行转化. 因为四边形ABCD是菱形,所以AC⊥BD.又因为PD⊥平面ABCD,所以PD⊥AC.因而AC⊥平面PDB,从而AC⊥DE.(2)设AC与BD相交于点F.连EF.由(1),知AC⊥平面PDB,所以AC⊥EF.所以S△ACE=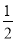 AC·EF,因此△ACE面积最小时,EF最小,则EF⊥PB.由△PDB∽△FEB,解得PD=
AC·EF,因此△ACE面积最小时,EF最小,则EF⊥PB.由△PDB∽△FEB,解得PD=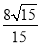 ,因为PD⊥平面ABCD,所以VP—ABCD=
,因为PD⊥平面ABCD,所以VP—ABCD=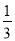 S□ABCD·PD=
S□ABCD·PD=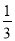 ×24×
×24×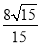 =
=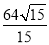 .
.
(1)证明:连接BD,设AC与BD相交于点F.
因为四边形ABCD是菱形,所以AC⊥BD.
又因为PD⊥平面ABCD,AC 平面ABCD,所以PD⊥AC.
平面ABCD,所以PD⊥AC.
而AC∩BD=F,所以AC⊥平面PDB.
E为PB上任意一点,DE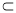 平面PBD,所以AC⊥DE.
平面PBD,所以AC⊥DE.
(2)连EF.由(1),知AC⊥平面PDB,EF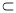 平面PBD,所以AC⊥EF. S△ACE=
平面PBD,所以AC⊥EF. S△ACE=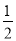 AC·EF,在△ACE面积最小时,EF最小,则EF⊥PB.
AC·EF,在△ACE面积最小时,EF最小,则EF⊥PB.
S△ACE=3,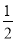 ×6×EF=3,解得EF=1.
×6×EF=3,解得EF=1.
由△PDB∽△FEB,得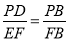 .由于EF=1,FB=4,
.由于EF=1,FB=4,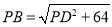 ,
,
所以PB=4PD,即 .解得PD=
.解得PD=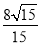
VP—ABCD=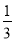 S□ABCD·PD=
S□ABCD·PD=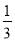 ×24×
×24×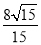 =
=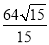 .
.
考点:线面垂直性质与判定定理,四棱锥体积


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二理科数学试卷(解析版) 题型:填空题
某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20 种,从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三下学期4月周练理科数学试卷(解析版) 题型:填空题
已知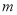 ,
,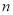 是空间中两条不同的直线,
是空间中两条不同的直线,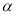 ,
,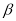 ,
,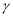 是空间中三个不同的平面,则下列命题正确的序号是 .
是空间中三个不同的平面,则下列命题正确的序号是 .
①若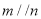 ,
,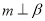 ,则
,则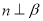 ; ②若
; ②若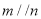 ,
,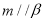 ,则
,则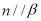 ;
;
③若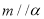 ,
,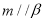 ,则
,则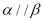 ; ④若
; ④若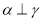 ,
,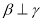 ,则
,则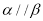 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高考模拟考试理科数学试卷(解析版) 题型:填空题
已知椭圆的中心在坐标原点O, A,C分别是椭圆的上下顶点,B是椭圆的左顶点,F是椭圆的左焦点,直线AF与BC相交于点D。若椭圆的离心率为 ,则∠BDF的正切值
,则∠BDF的正切值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com