Question

已知命题p：点A（x，y）在圆（x-1）²+（y-1）²=1外，若命题p是假命题，则z=x+y的最小值为

2

．

Answer 1

分析：由命题p：点A（x，y）在圆（x-1）²+（y-1）²=1外，且命题p是假命题，知点A（x，y）在圆（x-1）²+（y-1）²=1内或点A（x，y）在圆（x-1）²+（y-1）²=1上，由此利用线性规划能求出z=x+y的最小值．

解答：解：∵命题p：点A（x，y）在圆（x-1）²+（y-1）²=1外，
且命题p是假命题，
∴点A（x，y）在圆（x-1）²+（y-1）²=1内或点A（x，y）在圆（x-1）²+（y-1）²=1上，
如图，

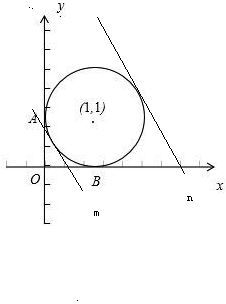
斜率为-1的切线m，n与圆有两个切点，其中m与圆的切点使得z取最小值，
n与圆的切点使得z取最大值，
∵O（0，0）与圆心（1，1）的斜率为k=1，
∴m，n与圆的切点分别是O（0，0）与圆心（1，1）的连线y=x与圆（x-1）²+（y-1）²=1的两个交点，
解方程组

y=x (x-1)2+(y-1)2=1

，得（1-

2

2

，1-

2

2

），（1+

2

2

，1+

2

2

）
∴在点（1-

2

2

，1-

2

2

）处，z=x+y取最小值2．
故答案为：2．

点评：本题考查命题的真假判断与应用，是基础题．解题时要认真审题，仔细解答，注意线性规划的合理运用．