【答案】
分析:(1)由题意可得,S(3)=N(1)+N(2)+N(3)+…+N(8),分别寻求每一项的值,然后可求
(2)先根据题意求出当n=1时,S(1)=N(1)+N(2),S(2)=N(1)+N(2)+N(3)+N(4),S(3)=N(1)+N(2)+N(3)+N(4)+…+N(8),S(4)=N(1)+N(2)+N(3)+N(4)+…+N(16),根据值出现的规律总结一般规律,然后可求
解答:解:(1)由题意可得,S(3)=N(1)+N(2)+N(3)+…+N(8)=1+1+3+1+5+3+7+1=22
(2)由题意可得,当n=1时,S(1)=N(1)+N(2)=1+1=2
当n=2时,S(2)=N(1)+N(2)+N(3)+N(4)=[N(1)+N(3)]+N(2×1)+N(4×1)=(1+3)+1+1
=2
2+2
当n=3时,S(3)=N(1)+N(2)+N(3)+N(4)+…+N(8)
=[N(1)+N(3)+N(5)+N(7)]+[N(2)+N(6)]+[N(4)+N(8)]
=(1+3+5+7)+(1+3)+(1+1)
=2
4+2
2+2
当n=4,S(4)=N(1)+N(2)+N(3)+N(4)+…+N(16)
=[N(1)+N(3)+N(5)+…+N(15)]+[N(2)+N(6)+N(10)+N(14)]+[N(4)+N(8)+N(12)+N(16)]
=(1+3+5+7+9+11+13+15)+(1+3+5+7)+(1+1+3+1)
=64+16+6
=2
6+2
4+2
2+2
n=5,S(5)=N(1)+N(2)+N(3)+…+N(32)
=[N(1)+N(3)+N(5)+…+N(31)]+[N(2)+N(6)+N(10)+…N(30)]+[N(4)+N(8)+…N(32)]
=(1+3+5++…+31)+(1+3+5+…+15)+(1+1+3+1+5+3+7+1)
=256+64+22=2
8+2
6+2
4+2
2+2
∴S(n)=N(1)+N(2)+N(3)+…+N(2
n)
=[N(1)+N(3)+N(5)+…+N(2
n-1)]+[N(2)+N(6)+N(10)+…N(2
n-2)]+[N(4)+N(8)+…N(2
n)]
=2
2n-2+2
2n-4+…+2
2+2
=
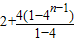
=2
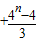
=
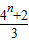
故答案为:22,
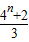 点评:
点评:本题以新定义为载体,主要考查了函数的函数值的求解,解题的关键是根据前几项的值寻求函数值出现的规律

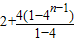
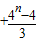 =
=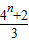
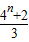




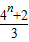 .
.