
【题目】在四棱锥![]() 中,底面是边长为4的菱形,
中,底面是边长为4的菱形,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
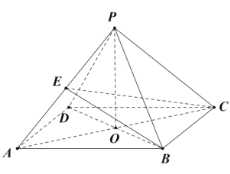
(1)证明:![]() ;
;
(2)若![]() 是
是![]() 的中点,
的中点,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据底面为菱形,以及![]() 平面
平面![]() ,可证得
,可证得![]() 面
面![]() ,从而证明
,从而证明![]() ;
;
(2)方法一:利用线面垂直,作出二面角的平面角.在直角三角形中,逐步求出边长,最终求出线面角.
方法二:根据建立的空间直角坐标系,写出点的坐标后,代入公式计算即可.
(1)因为底面是菱形,所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
![]() ,所以
,所以![]() 面
面![]() .
.
又![]() 面
面![]() ,所以
,所以![]() .
.
(2)由(1)
在![]() 中,
中,![]() ,∴
,∴![]() ,
,![]() ,
,
方法一:
过![]() 做
做![]() 于
于![]() ,连
,连![]() ,则
,则![]() ,
,
所以![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() .
.
所以![]() .
.
![]() ,
,
得![]() ,
,
![]() ,
,![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

方法二:
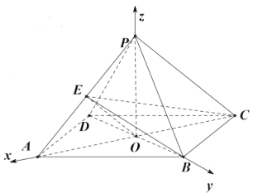
如图,以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设面![]() 的法向量为
的法向量为![]() ,
,
则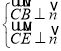 ,即
,即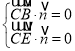 ,
,
即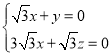 ,得方程的一组解为
,得方程的一组解为![]() ,
,![]() ,
,![]() ,
,
即![]() .
.
又面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以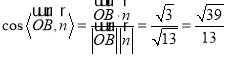 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】定义两个函数的关系:函数![]() 的定义域分别为
的定义域分别为![]() ,若对任意的
,若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,我们就称函数
,我们就称函数![]() 为
为![]() 的“子函数”.已知函数
的“子函数”.已知函数![]() ,
,![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 为
为![]() 的一个“子函数”,求
的一个“子函数”,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“水资源与永恒发展”是2015年联合国世界水资源日主题,近年来,某企业每年需要向自来水厂所缴纳水费约4万元,为了缓解供水压力,决定安装一个可使用4年的自动污水净化设备,安装这种净水设备的成本费(单位:万元)与管线、主体装置的占地面积(单位:平方米)成正比,比例系数约为0.2.为了保证正常用水,安装后采用净水装置净水和自来水厂供水互补的用水模式.假设在此模式下,安装后该企业每年向自来水厂缴纳的水费C(单位:万元)与安装的这种净水设备的占地面积x(单位:平方米)之间的函数关系是C(x)=![]() (x≥0,k为常数).记y为该企业安装这种净水设备的费用与该企业4年共将消耗的水费之和.
(x≥0,k为常数).记y为该企业安装这种净水设备的费用与该企业4年共将消耗的水费之和.
(1)试解释C(0)的实际意义,并建立y关于x的函数关系式并化简;
(2)当x为多少平方米时,y取得最小值,最小值是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,直线
,直线![]() :
:![]() 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆![]() 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.![]() 为左顶点,过点
为左顶点,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)以线段![]() 为直径的圆是否过定点?若是,写出所有定点的坐标;若不是,请说明理由.
为直径的圆是否过定点?若是,写出所有定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为多面体,平面
为多面体,平面![]() 与平面
与平面![]() 垂直,点
垂直,点![]() 在线段
在线段![]() 上,
上,![]()
![]() 都是正三角形.
都是正三角形.

(1)证明:直线![]() ∥面
∥面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值是
的余弦值是![]() ,若不存在请说明理由,若存在请求出
,若不存在请说明理由,若存在请求出![]() 点所在的位置。
点所在的位置。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据历年大学生就业统计资料显示:某大学理工学院学生的就业去向涉及公务员、教师、金融、商贸、公司和自主创业等六大行业.2020届该学院有数学与应用数学、计算机科学与技术和金融工程等三个本科专业,毕业生人数分别是70人,140人和210人.现采用分层抽样的方法,从该学院毕业生中抽取18人调查学生的就业意向.
(1)应从该学院三个专业的毕业生中分别抽取多少人?
(2)国家鼓励大学生自主创业,在抽取的18人中,含有“自主创业”就业意向的有6人,且就业意向至少有三个行业的学生有7人.为方便统计,将至少有三个行业就业意向的这7名学生分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计如下表:
,统计如下表:
学生 就业意向 |
|
|
|
|
|
|
|
公务员 | × | 〇 | × | 〇 | 〇 | × | × |
教师 | × | 〇 | × | 〇 | 〇 | 〇 | 〇 |
金融 | × | × | 〇 | 〇 | 〇 | × | × |
商贸 | 〇 | 〇 | 〇 | × | 〇 | 〇 | 〇 |
公司 | 〇 | 〇 | × | 〇 | 〇 | × | 〇 |
自主创业 | 〇 | × | 〇 | × | × | 〇 | 〇 |
其中“〇”表示有该行业就业意向,“×”表示无该行业就业意向.
①试估计该学院2020届毕业生中有自主创业意向的学生人数;
②现从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这7人中随机抽取2人接受采访,设
这7人中随机抽取2人接受采访,设![]() 为事件“抽取的2人中至少有一人有自主创业意向”,求事件
为事件“抽取的2人中至少有一人有自主创业意向”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com