
【题目】直角三角形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一个动点,且
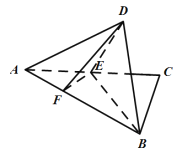
上一个动点,且![]() ,如图所示,沿
,如图所示,沿![]() 将
将![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
(1)当![]() 时,证明:
时,证明:![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析;(2)答案见解析.
【解析】试题分析:
(1)由题意可得![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,当
,当![]() 时,由几何关系可证得
时,由几何关系可证得![]() 平面
平面![]() .则
.则![]() .利用线面垂直的判断定理可得
.利用线面垂直的判断定理可得![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,结合直线的方向向量与平面的法向量计算可得存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
试题解析:
(1)在![]() 中,
中,![]() ,即
,即![]() ,
,
则![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,
当![]() 时,
时,![]() 是
是![]() 的中点,而
的中点,而![]() 是
是![]() 的中点,
的中点,
∴![]() 是
是![]() 的中位线,∴
的中位线,∴![]() .
.
在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,
∴![]() 是
是![]() 的中点.
的中点.
在![]() 中,
中,![]() ,
,
∴![]() ,则
,则![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴
,∴![]() .
.
而![]() ,∴
,∴![]() 平面
平面![]() .
.
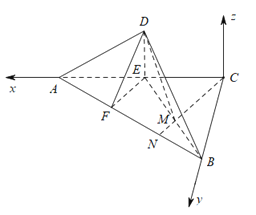
(2)以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立如图所示空间直角坐标系.
轴,建立如图所示空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 是
是![]() 中点,
中点,![]() ,而平面
,而平面![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() ,
,
则![]() .
.
假设存在满足题意的![]() ,则由
,则由![]() .
.
可得![]() ,
,
则![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则 即
即![]()
令![]() ,可得
,可得![]() ,
,![]() ,即
,即![]() .
.
∴![]() 与平面
与平面![]() 所成的角的正弦值
所成的角的正弦值
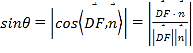
![]() .
.
解得![]() (
(![]() 舍去).
舍去).
综上,存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】某调查机构随机调查了![]() 岁到
岁到![]() 岁之间的
岁之间的![]() 位网上购物者的年龄分布情况,并将所得数据按照
位网上购物者的年龄分布情况,并将所得数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成
分成![]() 组,绘制成频率分布直方图(如图).
组,绘制成频率分布直方图(如图).
(1)求频率分布直方图中实数![]() 的值及这
的值及这![]() 位网上购物者中年龄在
位网上购物者中年龄在![]() 内的人数;
内的人数;
(2)现采用分层抽样的方法从参与调查的![]() 位网上购物者中随机抽取
位网上购物者中随机抽取![]() 人,再从这
人,再从这![]() 人中任选
人中任选![]() 人,设这
人,设这![]() 人中年龄在
人中年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() (
(![]() )的左焦点为
)的左焦点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且垂直于长轴的弦长为
且垂直于长轴的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 分别是椭圆的左、右顶点,若过点
分别是椭圆的左、右顶点,若过点![]() 的直线与椭圆相交于不同两点
的直线与椭圆相交于不同两点![]() 、
、![]() .
.
①求证:![]() ;
;
②求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计数据表明,样本中所有人每天用于阅读的时间(简称阅读用时)都不超过3小时,其频数分布表如下:(用时单位:小时)
用时分组 |
|
|
|
|
|
|
频数 | 10 | 20 | 50 | 60 | 40 | 20 |
(1)用样本估计总体,求该市市民每天阅读用时的平均值;
(2)为引导市民积极参与阅读,有关部门牵头举办市读书经验交流会,从这200人中筛选出男女代表各3名,其中有2名男代表和1名女代表喜欢古典文学.现从这6名代表中任选2名男代表和2名女代表参加交流会,求参加交流会的4名代表中,喜欢古典文学的男代表多于喜欢古典文学的女代表的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来随着素质教育的不断推进,高考改革趋势明显.国家教育部先后出台了有关高考的《学业水平考试》、《综合素质评价》、《加分项目瘦身与自主招生》三个重磅文件,引起社会极大关注,有人说:男孩苦,女孩乐!为了了解某地区学生和包括老师,家长在内的社会人士对高考改革的看法,某媒体在该地区选择了![]() 人,,就是否“赞同改革”进行调查,调查统计的结果如下表:
人,,就是否“赞同改革”进行调查,调查统计的结果如下表:
赞同 | 不赞同 | 无所谓 | |
在校学生 |
|
|
|
社会人士 |
|
|
|
已知在全体样本中随机抽取![]() 人,抽到持“不赞同”态度的人的概率为
人,抽到持“不赞同”态度的人的概率为![]() .
.
(1)现用分层抽样的方法在所有参与调查的人中抽取![]() 人进行问卷访谈,文应该在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,文应该在持“无所谓”态度的人中抽取多少人?
(2)在持“不赞同”态度的人中,用分层抽样方法抽取![]() 人,若从
人,若从![]() 人中任抽
人中任抽![]() 人进一步深入调查,为更多了解学生的意愿,要求在校学生人数不少于社会人士人士,求恰好抽到两名在校学生的概率.
人进一步深入调查,为更多了解学生的意愿,要求在校学生人数不少于社会人士人士,求恰好抽到两名在校学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱台被过点![]() 的平面截去一部分后得到如图所示的几何体,其下底面四边形
的平面截去一部分后得到如图所示的几何体,其下底面四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 与底面
与底面![]() 所成角的正切值为2,求二面角
所成角的正切值为2,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018湖南(长郡中学、株洲市第二中学)、江西(九江一中)等十四校高三第一次联考】已知函数![]() (其中
(其中![]() 且
且![]() 为常数,
为常数, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ).
).
(Ⅰ)若函数![]() 的极值点只有一个,求实数
的极值点只有一个,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,若
时,若![]() (其中
(其中![]() )恒成立,求
)恒成立,求![]() 的最小值
的最小值![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com