
【题目】已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A-BCD的外接球,BC=3,![]() ,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
【答案】![]()
【解析】
设△BDC的中心为O1,球O的半径为R,连接oO1D,OD,O1E,OE,可得R2=3+(3﹣R)2,解得R=2,过点E作圆O的截面,当截面与OE垂直时,截面的面积最小,当截面过球心时,截面面积最大,即可求解.
如图,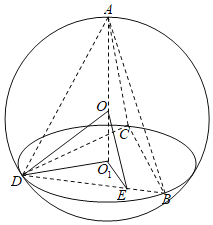
设△BDC的中心为O1,球O的半径为R,
连接oO1D,OD,O1E,OE,
则![]() ,AO1
,AO1![]()
在Rt△OO1D中,R2=3+(3﹣R)2,解得R=2,
∵BD=3BE,∴DE=2
在△DEO1中,O1E![]()
∴![]()
过点E作圆O的截面,当截面与OE垂直时,截面的面积最小,
此时截面圆的半径为![]() ,最小面积为2π.
,最小面积为2π.
当截面过球心时,截面面积最大,最大面积为4π.
故答案为:[2π,4π]


科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0).且点C与点D在函数f(x)=  的图象上.若在矩形ABCD内随机取一点,则该点取自空白部分的概率等于( )
的图象上.若在矩形ABCD内随机取一点,则该点取自空白部分的概率等于( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件.今年拟下调销售单价以提高销量增加收益.据估算,若今年的实际销售单价为![]() 元/件
元/件![]() ,则新增的年销量
,则新增的年销量![]() (万件).
(万件).
(Ⅰ)写出今年商户甲的收益![]() (单位:万元)与
(单位:万元)与![]() 的函数关系式;
的函数关系式;
(Ⅱ)商户甲今年采取降低单价提高销量的营销策略,是否能获得比往年更大的收益(即比往年收益更多)?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1,(a>b>0)的离心率为
=1,(a>b>0)的离心率为 ![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+ ![]() =0)且不垂直于x轴直线l椭圆C相交于A、B两点. (Ⅰ)求椭圆C的方程;
=0)且不垂直于x轴直线l椭圆C相交于A、B两点. (Ⅰ)求椭圆C的方程;
(Ⅱ)求 ![]()
![]() 取值范围;
取值范围;
(Ⅲ)若B关于x轴的对称点是E,证明:直线AE与x轴相交于定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心均在原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2 , 这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1、e2 , 则e1e2的取值范围为( )
A.![]()
B.![]()
C.(2,+∞)
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,则下列命题正确的是 . (填写所有正确命题的序号) ①若sinAsinB=2sin2C,则0<C< ![]() ;
;
②若a+b>2c,则0<C< ![]() ;
;
③若a4+b4=c4 . 则△ABC为锐角三角形;
④若(a+b)c<2ab,则C> ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com