
【题目】设集合A={x|1≤x≤4},B={x|m≤x≤m+1}.
(1)当m=3时,求A∩B与A∩RB;
(2)若A∩B=B,求实数m的取值范围.
【答案】
(1)解:m=3时,B={x|3≤x≤4}.A∩B=[3,4].
RB=(﹣∞,3)∪(4,+∞);
A∩RB=[1,3)
(2)解:∵A∩B=B,∴BA.
∴ ![]() ,解得1≤m≤3.
,解得1≤m≤3.
∴实数m的取值范围是[1,3]
【解析】(1)m=3时,B={x|3≤x≤4}.利用交集的运算性质即可得出A∩B.利用补集的运算性质可得RB=(﹣∞,3)∪(4,+∞),即可得出A∩RB.(2)A∩B=B,考点BA.考点 ![]() ,解得m范围.
,解得m范围.
【考点精析】本题主要考查了交、并、补集的混合运算的相关知识点,需要掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
)x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为减函数.
其中正确命题的序号为: .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,离心率为
的左、右焦点,离心率为![]() ,
,![]() 分别是椭圆的上、下顶点,
分别是椭圆的上、下顶点,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作直线与
作直线与![]() 交于
交于![]() 两点,求三角形
两点,求三角形![]() 面积的最大值(
面积的最大值(![]() 是坐标原点).
是坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 方程为
方程为![]() ,双曲线
,双曲线![]() 的两条渐近线分别为
的两条渐近线分别为![]() ,
, ![]() ,过椭圆
,过椭圆![]() 的右焦点作直线
的右焦点作直线![]() ,使
,使![]() ,又
,又![]() 与
与![]() 交于点
交于点![]() ,设直线
,设直线![]() 与椭圆
与椭圆![]() 的两个交点由上至下依次为
的两个交点由上至下依次为![]() ,
, ![]() .
.
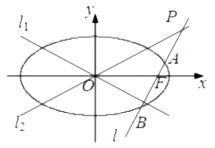
(1)若![]() 与
与![]() 所成的锐角为
所成的锐角为![]() ,且双曲线的焦距为4,求椭圆
,且双曲线的焦距为4,求椭圆![]() 的方程;
的方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax+(k﹣1)a﹣x(a>且a≠1)是定义域为R的奇函数.
(1)求k值;
(2)若f(1)>0,试判断函数单调性,并求使不等式f(x2+x)+f(t﹣2x)>0恒成立的t的取值范围;
(3)若f(1)= ![]() ,设g(x)=a2x+a﹣2x﹣2mf(x),g(x)在[1,+∞)上的最小值为﹣1,求m的值.
,设g(x)=a2x+a﹣2x﹣2mf(x),g(x)在[1,+∞)上的最小值为﹣1,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
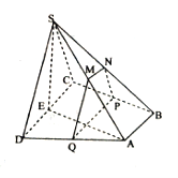
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,过
的中点,过![]() 作平面
作平面![]() 分别与交
分别与交![]() 于点
于点![]() .
.
(Ⅰ)当![]() 为
为![]() 中点时,求证:平面
中点时,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com