
【题目】已知函数f(x)=|x﹣l|+|x﹣3|.
(1)解不等式f(x)≤6;
(2)若不等式f(x)≥ax﹣1对任意x∈R恒成立,求实数a的取值范围.
【答案】
(1)解:函数f(x)=|x﹣l|+|x﹣3|= 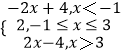 的图象如图所示,
的图象如图所示,
不等式f(x)≤6,即 ![]() ①或
①或 ![]() ②,或
②,或 ![]() ③.
③.
解①求得x∈,解②求得3<x≤5,解③求得﹣1≤x≤3.
综上可得,原不等式的解集为[﹣1,5].
(2)解:若不等式f(x)≥ax﹣1对任意x∈R恒成立,则函数f(x)的图象
不能在y=ax﹣1的图象的下方.
如图所示:
由于图中两题射线的斜率分别为﹣2,2,点B(3,2),
∴3a﹣1≤2,且 a≥﹣2,求得﹣2≤a≤1.

【解析】(1)把不等式f(x)≤6等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.(2)由题意可得函数f(x)的图象不能在y=ax﹣1的图象的下方,数形结合求得a的范围.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() ,直线
,直线![]() 与抛物线C交于A,B两点.
与抛物线C交于A,B两点.
(1)若直线![]() 过抛物线C的焦点,求
过抛物线C的焦点,求![]() .
.
(2)已知抛物线C上存在关于直线![]() 对称的相异两点M和N,求
对称的相异两点M和N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(﹣1,
=1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(﹣1, ![]() ).过椭圆E内一点P(1,
).过椭圆E内一点P(1, ![]() )的两条直线分别与椭圆交于点A、C和B、D,且满足
)的两条直线分别与椭圆交于点A、C和B、D,且满足 ![]() ,其中λ为实数.当直线AP平行于x轴时,对应的λ=
,其中λ为实数.当直线AP平行于x轴时,对应的λ= ![]() .
. 
(1)求椭圆E的方程;
(2)当λ变化时,kAB是否为定值?若是,请求出此定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某机器人的运动轨道是边长为1米的正三角形ABC,开机后它从A点出发,沿轨道先逆时针运动再顺时针运动,每运动6米改变一次运动方向(假设按此方式无限运动下去),运动过程中随时记录逆时针运动的总路程s1和顺时针运动的总路程s2,x为该机器人的“运动状态参数”,规定:逆时针运动时x=s1,顺时针运动时x=-s2,机器人到A点的距离d与x满足函数关系d=f(x),现有如下结论:
①f(x)的值域为[0,1];
②f(x)是以3为周期的函数;
③f(x)是定义在R上的奇函数;
④f(x)在区间[-3,-2]上单调递增.
其中正确的有_________(写出所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明{an+ ![]() }是等比数列,并求{an}的通项公式;
}是等比数列,并求{an}的通项公式;
(2)证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com