
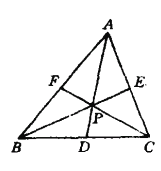
【题目】如图,![]() 的三条内线段
的三条内线段![]() 、
、![]() 、
、![]() 交于点
交于点![]() 、用红、蓝两种颜色对
、用红、蓝两种颜色对![]() 的三条边线和三条内线段染色,使同色的三线不交于一点.证明:在图中所有的三角形中,至少存在两个同色三角形,且它的各边或延长线被另一线截得的两线段之比的和大于3.
的三条边线和三条内线段染色,使同色的三线不交于一点.证明:在图中所有的三角形中,至少存在两个同色三角形,且它的各边或延长线被另一线截得的两线段之比的和大于3.
【答案】见解析
【解析】
根据抽屉原理,在三条边线和二条线这6条线中,至少有3条是同色的,设共为红色.则红线的条数为5,4或3.
(1)若有5条红线,则必有3条红线交于一点,不合题意.
(2)若有4条红线,可分两类:
(i)如果3条是边线.1条是内线或1条边线、3条内线时,则都存在3条红线交于一点,不合题意.
(ii)如果边线和内线各有两条时,不妨没边线为![]() 、
、![]() ,则内线只能是
,则内线只能是![]() 、
、![]() .这时
.这时![]() 、
、![]() 都是红色三角形,它们分别被直线
都是红色三角形,它们分别被直线![]() 、
、![]() 所截.
所截.
若![]() 被直线
被直线![]() 所截.由梅氏定理.有
所截.由梅氏定理.有![]() .
.
由均值不等式,得![]() .
.
因为![]() 下成立,所以上式等号不能成立.
下成立,所以上式等号不能成立.
故![]() .
.
(3)若有3条红线,可分三类:
(i)如果3条都为边线或都为内线时,显然都不符合题意.
(ii)如果两条为边线,1条为内线时,设边线为![]() 、
、![]() ,则内线必为
,则内线必为![]() 或
或![]() .不妨设为
.不妨设为![]() .此时
.此时![]() 为红色三角形,
为红色三角形,![]() 为蓝色三角形,结论成立.
为蓝色三角形,结论成立.
(iii)如果1条为边线,两条为内线时,相当于两条边线为蓝线.1条内线为蓝线,由(ii)知,结论成立.
综合(1)、(2)、(3)知,命题成立.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
【题目】如图,等边三角形![]() 的中线
的中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,下列命题中,错误的是
旋转过程中的一个图形,下列命题中,错误的是

A. 恒有![]() ⊥
⊥![]()
B. 异面直线![]() 与
与![]() 不可能垂直
不可能垂直
C. 恒有平面![]() ⊥平面
⊥平面![]()
D. 动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个正多边形的每条边和对角线恰各染成2018种颜色之一,且所有边及对角线不全同色.若正多边形中不存在两色三角形(即三角形的三边恰被染成两种颜色),则称该多边形的染色是“和谐的”.求最大的正整数![]() ,使得存在一个和谐的染色正
,使得存在一个和谐的染色正![]() 边形.
边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
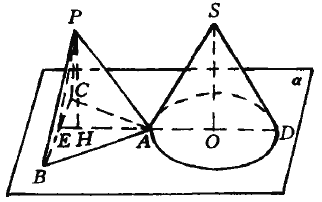
【题目】如图,三棱锥![]() 的底面
的底面![]() 与圆锥
与圆锥![]() 的底面
的底面![]() 都在平面
都在平面![]() 上,且
上,且![]() 过点
过点![]() ,又
,又![]() 的直径
的直径![]() ,垂足为
,垂足为![]() .设三棱锥
.设三棱锥![]() 的所有棱长都是1,圆锥的底面直径与母线长也都是1,圆锥的底面直径与母线长也都是1.求圆锥的顶点
的所有棱长都是1,圆锥的底面直径与母线长也都是1,圆锥的底面直径与母线长也都是1.求圆锥的顶点![]() 到三棱锥
到三棱锥![]() 的三个侧面的距离.
的三个侧面的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县位于沙漠地带,人与自然长期进行顽强的斗争,到1996年底全县的绿化率已达到30%(成为绿洲).从1997年开始,每年将出现这样的局面,原有沙漠面积的16%被栽上树,改造为绿洲,而同时,原有绿洲面积的4%又被侵蚀,变为沙漠.
(1)设全县面积为1,1996年底绿洲面积为![]() ,经过
,经过![]() 年绿洲面积为
年绿洲面积为![]() .求证:
.求证:![]() .
.
(2)至少需经过多少年的努力才能使全县的绿化率超过60%(年取整数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域D={x|x≠0},且满足对于任意x1,x2∈D.有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明;
(3)如果f(4)=1,f(3x+1)+f(2x-6)≤3,且f(x)在(0,+∞)上是增函数,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | |||
女生 | |||
合计 | 120 |
(2)从被调查中对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com