
【题目】己知{an}是等差数列,其前n项和Sn=n2﹣2n+b﹣1,{bn}是等比数列,其前n项和Tn![]() ,则数列{ bn +an}的前5项和为( )
,则数列{ bn +an}的前5项和为( )
A.37B.-27C.77D.46
【答案】C
【解析】
由等差数列的求和公式、等比数列的求和公式,结合数列的递推式,可得b=1,a=2,求得数列{an},{bn}的通项公式,再由数列的分组求和,结合等差数列和等比数列的求和公式,可得所求和.
{an}是等差数列,其前n项和![]() ,
,
由等差数列的求和公式可得b﹣1=0,即b=1,
即Sn=n2﹣2n,
a1=S1=﹣1,an=Sn﹣Sn﹣1=n2﹣2n﹣(n﹣1)2+2(n﹣1)=2n﹣3,
则an=2n﹣3,n∈N*;
{bn}是等比数列,其前n项和![]() ,
,
则b1![]() 3,bn=Tn﹣Tn﹣1
3,bn=Tn﹣Tn﹣1![]() 3n
3n![]() 3n﹣1=﹣23n﹣1,
3n﹣1=﹣23n﹣1,
则![]() 3=﹣2,即a=2,
3=﹣2,即a=2,
则bn +an=n+2n,
数列{ bn +an}的前5项和为(1+2+…+5)+(2+4+…+32)
![]() 5×6
5×6![]() 77.
77.
故选:C.


科目:高中数学 来源: 题型:
【题目】某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建房防辐射材料的选用与宿舍到工厂距离有关.若建造宿舍的所有费用p(万元)和宿舍与工厂的距离x(km)的关系为![]() ,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
(1)求f(x)的表达式
(2)宿舍应建在离工厂多远处,可使总费用f(x)最小并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】业界称“中国芯”迎来发展和投资元年,某芯片企业准备研发一款产品,研发启动时投入资金为![]() (
(![]() 为常数)元,之后每年会投入一笔研发资金,
为常数)元,之后每年会投入一笔研发资金,![]() 年后总投入资金记为
年后总投入资金记为![]() ,经计算发现当
,经计算发现当![]() 时,
时,![]() 近似地满足
近似地满足![]() ,其中
,其中![]() 为常数,
为常数,![]() .已知
.已知![]() 年后总投入资金为研发启动时投入资金的
年后总投入资金为研发启动时投入资金的![]() 倍.问
倍.问
(1)研发启动多少年后,总投入资金是研发启动时投入资金的![]() 倍;
倍;
(2)研发启动后第几年的投入资金的最多.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知![]() ,
,![]() ,Q到海岸线OM,ON的距离分别为3 km,
,Q到海岸线OM,ON的距离分别为3 km,![]() km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.
km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.
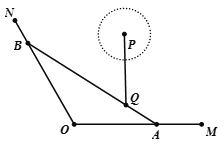
(1)求水上旅游线AB的长;
(2)若小岛正北方向距离小岛6 km处的海中有一个圆形强水波P,从水波生成t h时的半径为![]() (a为大于零的常数).强水波开始生成时,一游轮以
(a为大于零的常数).强水波开始生成时,一游轮以![]() km/h的速度自码头A开往码头B,问实数a在什么范围取值时,强水波不会波及游轮的航行.
km/h的速度自码头A开往码头B,问实数a在什么范围取值时,强水波不会波及游轮的航行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为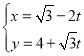 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)设点P为曲线C上的动点,点M,N为直线![]() 上的两个动点,若
上的两个动点,若![]() 是以
是以![]() 为直角的等腰三角形,求
为直角的等腰三角形,求![]() 直角边长的最小值.
直角边长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,四边形ABCD菱形,![]() ,平面
,平面![]() 平面 ABCD,
平面 ABCD,![]() .E,F 分别是线段 SC,AB 上的一点,
.E,F 分别是线段 SC,AB 上的一点, ![]() .
.
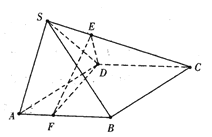
(1)求证:![]() 平面SAD;
平面SAD;
(2)求平面DEF与平面SBC所成锐二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】金石文化,是中国悠久文化之一.“金”是指“铜”,“石”是指“石头”,“金石文化”是指在铜器或石头上刻有文字的器件.在一千多年前,有一种凸多面体工艺品,是金石文化的代表作,此工艺品的三视图是三个全等的正八边形(如图),若一个三视图(即一个正八边形)的面积是![]() ,则该工艺品共有______个面,表面积是______.
,则该工艺品共有______个面,表面积是______.
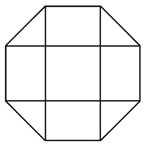
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com