
����Ŀ��ij��˾��Ͷ��һ���²�Ʒ�������㣬��֪ÿ������![]() ����ĸ��ֲ�Ʒ����Ҫ���ܳɱ�
����ĸ��ֲ�Ʒ����Ҫ���ܳɱ�![]() ����Ԫ�������ݲ�Ʒ�ߴ磬��Ʒ��Ʒ�ʿ��ܳ����š��С�����������������ȡ��1000����Ʒ�����ߴ磬�ߴ�ֱ���
����Ԫ�������ݲ�Ʒ�ߴ磬��Ʒ��Ʒ�ʿ��ܳ����š��С�����������������ȡ��1000����Ʒ�����ߴ磬�ߴ�ֱ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����
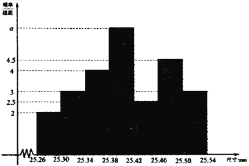
����λ��![]() ���У���ͳ�Ƶõ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
���У���ͳ�Ƶõ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
��Ʒ��Ʒ���������Ӧ�ļ۸�![]() ��Ԫ/�����������
��Ԫ/�����������![]() ֮��ĺ�����ϵ���±���ʾ.
֮��ĺ�����ϵ���±���ʾ.
��ƷƷ�� | ��Ʒ�ߴ�ķ�Χ | �۸� |
�� |
|
|
�� |
|
|
�� |
|
|
��Ƶ����Ϊ���ʽ���������⣺
��1����ʵ��![]() ��ֵ��
��ֵ��
��2��������![]() ȷ��ʱ���費ͬƷ�ʵIJ�Ʒ�۸�Ϊ�������
ȷ��ʱ���費ͬƷ�ʵIJ�Ʒ�۸�Ϊ�������![]() �����������
�����������![]() �ķֲ��У�
�ķֲ��У�
��3�����Ƶ������![]() Ϊ��ֵʱ���ù�˾���������������ֵ.
Ϊ��ֵʱ���ù�˾���������������ֵ.
���𰸡���1��![]() ����2����������3�������
����2����������3�������![]() ʱ���ù�˾������ȡ�����ֵ���������Ϊ138��.
ʱ���ù�˾������ȡ�����ֵ���������Ϊ138��.
��������
��1��������Ƶ�ʷֲ�ֱ��ͼ������С���ε������Ϊ1���������ʵ��![]() ��ֵ��
��ֵ��
��2���ֱ��������ƷƷ��Ϊ�š�Ϊ�С�Ϊ��ʱ��Ƶ�ʣ�Ȼ�����˷ֲ��У�
��3���������⣬�õ��ù�˾������ĺ�����ϵʽ��Ȼ�����õ��������˾���������ֵ.
�⣺��1���������![]() �����
�����![]() ��
��
��2������ƷƷ��Ϊ��ʱƵ��Ϊ![]() ����ʱ�۸�Ϊ
����ʱ�۸�Ϊ![]() ��
��
����ƷƷ��Ϊ��ʱƵ��Ϊ![]() ����ʱ�۸�Ϊ
����ʱ�۸�Ϊ![]() ��
��
����ƷƷ��Ϊ��ʱƵ��Ϊ![]() ����ʱ�۸�Ϊ
����ʱ�۸�Ϊ![]() ��
��
��Ƶ����Ϊ���ʣ��ɵ��������![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
|
|
|
|
| 0.5 | 0.2 | 0.3 |
��3���蹫˾������Ϊ![]() ����
����
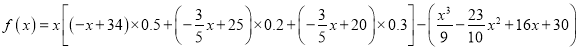 ������
������![]() ��
��
![]()
��Ȼ��![]() ʱ��
ʱ��![]() ��
��![]() ʱ��
ʱ��![]() ��
��
�൱�����![]() ʱ��
ʱ��![]() ȡ�����ֵ.
ȡ�����ֵ.![]()
���Ƶ������![]() ʱ���ù�˾������ȡ�����ֵ���������Ϊ138��.
ʱ���ù�˾������ȡ�����ֵ���������Ϊ138��.


 ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f ��x��=ax��ex��a��R����g��x��=![]() ��
��
����������f ��x���ĵ������䣻
������x0����0��+������ʹ����ʽf ��x����g��x����ex��������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��˫ʮһ�����Ļ����è�������268����λ��ʮ��Ԫ������ң���ͬ�����ٴ��¸ߣ���ȥ��218��ʮ��Ԫ������50��ʮ��Ԫ������Щ���ֵı�������������������ı��֣����ǹ��ﳵ���й������ѵ��漣��Ϊ���о��������۶�ı仯���ƣ�һ����ͳ����2010�굽2019����è˫ʮһ�����۶�����![]() ����λ��ʮ��Ԫ��.�������±�1��
����λ��ʮ��Ԫ��.�������±�1��
��1
��� | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
���۶� | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
�����������ݻ���ɢ��ͼ����ͼ��ʾ.
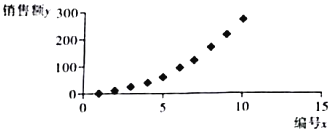
�����۳���100��ʮ��Ԫ������ݽ������������������۶��200��ʮ��Ԫ������ݽ�������������2010�굽2019����ʮ�����������������ȡ2����������ȡ��һ�����������ĸ���.
�ο���ʽ������һ������![]() ��
��![]() ������
������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ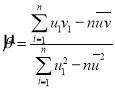 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019����ף�л���������70�����ı�ʽ�������л������վ����������������ǿ����������׳־.�ı�ʽ��ģ֮������֮ȫ������ʷ֮�����֮�¡�Ҫ��֮ȫ����ǿ���ɾ�.װ��������ǿ����������ǿ��֮��������֤�����������������һ�����ӵļᶨ����.�˴δ��ı������õ���ȫ�й��˵Ĺ�ע�����õ�����������˵Ĺ�ע.ij��λ��10λ����ˣ����й�ע�˴δ��ı�����8λ��������10λ�����������ѡȡ3λ��һ�βɷã��ɷ�����������2λ��ע�˴δ��ı��ĸ���Ϊ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ǿ���dz�������Ϊ��������������֣�����ͨ6������˽�ҳ�Ͷ����ǿ�յ�һ��ķ��ã������ѣ�ͳһΪaԪ������һ������ʱ��ʵ�е��Ƿ��ʸ������ƣ���������һ��ȳ���������·��ͨ�¹ʵ��������ϵ��������ͨ�¹ʵĴ���Խ�࣬����Ҳ��Խ�ߣ����帡��������±���
��ǿ�ո������غ������ʱ��ʱ� | ||
�������� | �������� | |
| ��һ���δ���������ε�·��ͨ�¹� | �¸�10% |
| �������δ���������ε�·��ͨ�¹� | �¸� |
| �������δ���������ε�·��ͨ�¹� | �¸�30% |
| ��һ����ȷ���һ�������β��漰�����ĵ�·��ͨ�¹� | 0% |
| ��һ����ȷ������μ��������������β��漰�����ĵ�·��ͨ�¹� | �ϸ�10% |
| ��һ����ȷ��������ν�ͨ�����¹� | �ϸ�30% |
ij����Ϊ�˽�ijһƷ����ͨ6������˽�ҳ���Ͷ������������ȡ��
���� | A1 | A2 | A3 | A4 | A5 | A6 |
���� | 10 | 5 | 5 | 20 | 15 | 5 |
����60����Ʒ�Ƴ���Ͷ�����͵�Ƶ�ʴ���һ����Ͷ�����͵ĸ��ʣ�����������⣺
��1�������ҹ�����������ͨ�¹�����ǿ�Ʊ���������������ǿ�ռ۸�Ĺ涨��![]() ����
����![]() Ϊijͬѧ�ҵ�һ����Ʒ�Ƴ��ڵ���������ʱ�ķ��ã���
Ϊijͬѧ�ҵ�һ����Ʒ�Ƴ��ڵ���������ʱ�ķ��ã���![]() �ķֲ�������ѧ����������ѧ����ֵ��������λ���֣�
�ķֲ�������ѧ����������ѧ����ֵ��������λ���֣�
��2��ij���ֳ�������ר��������һƷ�ƵĶ��ֳ����ҽ���һ��Ľ�ǿ�ձ��Ѹ��ڻ������ѵij�����Ϊ�¹ʳ������蹺��һ���¹ʳ�����5000Ԫ��һ�����¹ʳ�ӯ��10000Ԫ:
�����������̹�������(������������)��Ʒ�ƶ��ֳ���������������������һ���¹ʳ��ĸ��ʣ�
������������һ�ι���100��(������������)��Ʒ�ƶ��ֳ�������������������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �Ǻ���
�Ǻ���![]() �������һ���Ӽ���������
�������һ���Ӽ���������![]() ��ʹ��
��ʹ��![]() ���������
���������![]() ��
��![]() ��һ���������㡱��Ҳ��
��һ���������㡱��Ҳ��![]() ������
������![]() �ϴ��������㣬��֪
�ϴ��������㣬��֪![]() ��
��![]() .
.
��1����![]() ������
������![]() �������㣻
�������㣻
��2��������![]() ������
������![]() �ϴ��������㣬��ʵ��
�ϴ��������㣬��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �ϵ�ż����
�ϵ�ż����![]() ����
����![]() ����
����![]() ʱ��
ʱ��![]() ������
������![]() ��
��![]() �ϵ��������֮��Ϊ�� ��
�ϵ��������֮��Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڰ뾶Ϊ![]() ��������һ�ڽ������������ĵ�����������ǡ�ö���ͬһ����Բ�ϣ�һ�������������һ����������������˶���������������أ��������·����________
��������һ�ڽ������������ĵ�����������ǡ�ö���ͬһ����Բ�ϣ�һ�������������һ����������������˶���������������أ��������·����________
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com