
若函数 同时满足:(ⅰ)对于定义域内的任意
同时满足:(ⅰ)对于定义域内的任意 ,恒有
,恒有 ;(ⅱ)对于定义域内的任意
;(ⅱ)对于定义域内的任意 ,当
,当 时,恒有
时,恒有 ,则称函数
,则称函数 为“二维函数”.现给出下列四个函数:
为“二维函数”.现给出下列四个函数:
① ;②
;② ;③
;③ ;④
;④
其中能被称为“二维函数”的有_____________(写出所有满足条件的函数的序号).
科目:高中数学 来源:2013-2014学年湖南汝城第一中学、长沙实验中学高三11月联考理数学卷(解析版) 题型:填空题
若函数 同时满足下列条件,(1)在D内为单调函数;(2)存在实数
同时满足下列条件,(1)在D内为单调函数;(2)存在实数 ,
,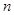 .当
.当 时,
时, ,则称此函数为D内的等射函数,设
,则称此函数为D内的等射函数,设
 则:
则:
(1)  在(-∞,+∞)的单调性为 (填增函数或减函数);(2)当
在(-∞,+∞)的单调性为 (填增函数或减函数);(2)当 为R内的等射函数时,
为R内的等射函数时, 的取值范围是
.
的取值范围是
.
查看答案和解析>>
科目:高中数学 来源:2015届福建省三明市高一第一次段考数学试卷(解析版) 题型:填空题
若函数 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意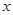 ,恒有
,恒有 ②对于定义域上的任意
②对于定义域上的任意 ,当
,当 时,恒有
时,恒有 ,则称函数
,则称函数 为
为
“理想函数”。给出下列四个函数中:⑴
 ⑵
⑵ 
 ⑶
⑶ 
⑷  ,能被称为“理想函数”的有_ _ (填相应的序号) 。
,能被称为“理想函数”的有_ _ (填相应的序号) 。
查看答案和解析>>
科目:高中数学 来源:2015届江西省高一上学期期中训练数学试卷(解析版) 题型:填空题
若函数 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意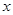 ,恒有
,恒有 ②对于定义域上的任意
②对于定义域上的任意 ,当
,当 时,恒有
时,恒有 ,则称函数
,则称函数 为“理想函数”。给出下列四个函数中:⑴
为“理想函数”。给出下列四个函数中:⑴
 ⑵
⑵ 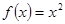
 ⑶
⑶ 
⑷  ,能被称为“理想函数”的有_ _ (填相应的序号) 。
,能被称为“理想函数”的有_ _ (填相应的序号) 。

查看答案和解析>>
科目:高中数学 来源:2014届湖北省高一上学期期末考试文科数学 题型:选择题
若函数 同时满足下列三个性质:①最小正周期为
同时满足下列三个性质:①最小正周期为 ;②图象关于直线
;②图象关于直线 对称;③在区间
对称;③在区间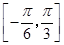 上是增函数.则
上是增函数.则 的解析式可以是
的解析式可以是
A. B.
B.
C. D.
D.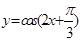
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com