
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求二面角F﹣BE﹣D的余弦值.

【答案】(1)见解析(2) ![]()
【解析】试题分析:(Ⅰ)因为DE⊥平面ABCD,所以DE⊥AC.因为ABCD是正方形,所以AC⊥BD,从而AC⊥平面BDE;(Ⅱ)建立空间直角坐标系D-xyz,分别求出平面BEF的法向量为![]() 和平面BDE的法向量,利用向量法能求出二面角的余弦值
和平面BDE的法向量,利用向量法能求出二面角的余弦值
试题解析:(1)证明:因为DE⊥平面ABCD,AC平面ABCD,所以DE⊥AC. 因为ABCD是正方形,所以AC⊥BD.
又BD,DE相交且都在平面BDE内,从而AC⊥平面BDE.
(2)因为DA,DC,DE两两垂直,所以建立空间直角坐标系Dxyz,如图所示.
因为DE⊥平面ABCD,所以BE与平面ABCD所成角就是∠DBE.已知BE与平面ABCD所成角为60°,所以∠DBE=60°,所以![]()
由AD=3可知DE=3![]() ,AF=
,AF=![]() .
.
由A(3,0,0),F(3,0, ![]() ),E(0,0,3
),E(0,0,3![]() ),B(3,3,0),C(0,3,0),
),B(3,3,0),C(0,3,0),
得=(0,-3, ![]() ),=(3,0,-2
),=(3,0,-2![]() ).设平面BEF的法向量为n=(x,y,z),
).设平面BEF的法向量为n=(x,y,z),
则即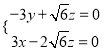 令z=
令z=![]() ,则n=(4,2,
,则n=(4,2, ![]() ).
).
因为AC⊥平面BDE,所以为平面BDE的法向量m=(3,-3,0),
所以cos〈n,m〉=![]() =
=![]() .
.
因为二面角为锐角,所以二面角FBED的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述不正确的是 ( )

A. 各月的平均最低气温都在0℃以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于20℃的月份有5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的![]() 位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下图所示.
位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下图所示.

(Ⅰ)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在40岁以上(含40岁)的市民人数;
(Ⅱ)若按分层抽样的方法从年龄在![]() 以内及
以内及![]() 以内的市民中随机抽取5人,再从这5人中随机抽取2人进行调研,求抽取的2人中,至多1人年龄在
以内的市民中随机抽取5人,再从这5人中随机抽取2人进行调研,求抽取的2人中,至多1人年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十一”期间,某淘宝店主对其商品的上架时间![]() (分钟)和销售量
(分钟)和销售量![]() (件)的关系作了统计,得到如下数据:
(件)的关系作了统计,得到如下数据:

经计算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)从满足![]() 的数据
的数据![]() 中任取两个,求所得两个数据都满足
中任取两个,求所得两个数据都满足![]() 的概率;
的概率;
(2)该店主通过作散点图,发现上架时间与销售量线性相关,请你帮助店主求出上架时间与销售量的线性回归方程(保留三位小数),并预测商品上架1000分钟时的销售量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个动圆与两个定圆![]() 和
和![]() 均相切,其圆心的轨迹为曲线C.
均相切,其圆心的轨迹为曲线C.
(1) 求曲线C的方程;
(2) 过点F(![]() )做两条可相垂直的直线
)做两条可相垂直的直线![]() ,设
,设![]() 与曲线C交于A,B两点,
与曲线C交于A,B两点, ![]() 与曲线 C交于C,D两点,线段AC,BD分别与直线
与曲线 C交于C,D两点,线段AC,BD分别与直线![]() 交于M,M,N两点。求证|MF|:|NF|为定值.
交于M,M,N两点。求证|MF|:|NF|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左顶点
的左顶点![]() ,且点
,且点![]() 在椭圆上,
在椭圆上, ![]() 分别是椭圆的左、右焦点。过点
分别是椭圆的左、右焦点。过点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标;
的坐标;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b分别是△ABC内角A,B的对边,且bsin2A=![]() acos Asin B,函数f(x)=sin Acos2x-sin2
acos Asin B,函数f(x)=sin Acos2x-sin2![]() sin 2x,x∈
sin 2x,x∈![]() .
.
(1)求A;
(2)求函数f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com