
 与双曲线
与双曲线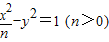 有相同的焦点F1、F2,P是两曲线的一个交点,则△F1PF2的面积是( )
有相同的焦点F1、F2,P是两曲线的一个交点,则△F1PF2的面积是( )
 ,双曲线的实轴长为2
,双曲线的实轴长为2 ,由它们有相同的焦点,得到m-n=2.不妨设m=5,n=3,根据双曲线和椭圆的定义可得|PF1|+|PF2|=2
,由它们有相同的焦点,得到m-n=2.不妨设m=5,n=3,根据双曲线和椭圆的定义可得|PF1|+|PF2|=2 ,|PF1|-|PF2|=2
,|PF1|-|PF2|=2 ,△PF1F2 中,由三边的关系得出其为直角三角形,由△PF1F2的面积公式即可运算得到结果.
,△PF1F2 中,由三边的关系得出其为直角三角形,由△PF1F2的面积公式即可运算得到结果. ,双曲线的实轴长为2
,双曲线的实轴长为2 ,
,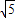 ,双曲线的实轴长为2
,双曲线的实轴长为2 ,
, ①
① ②
② •PF1•PF2=
•PF1•PF2= (
(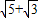 )(
)( )=1
)=1

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源:2014届河南安阳一中高二第一次阶段测试理科数学试卷(解析版) 题型:选择题
若椭圆 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,
, 是两曲线的一个交点,则
是两曲线的一个交点,则 等于
( )
等于
( )
A.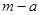 B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2004-2005学年重庆一中高二(上)期末数学试卷(文科)(解析版) 题型:选择题
 与双曲线
与双曲线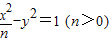 有相同的焦点F1、F2,P是两曲线的一个交点,则△F1PF2的面积是( )
有相同的焦点F1、F2,P是两曲线的一个交点,则△F1PF2的面积是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com