
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】类比平面几何中的定理:△ABC中,若DE是△ABC的中位线,则有S△ADE∶S△ABC=1∶4;若三棱锥A-BCD有中截面EFG∥平面BCD,则截得三棱锥的体积与原三棱锥体积之间的关系式为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
转速x(转/秒) | 2 | 4 | 5 | 6 | 8 |
每小时生产有缺点的零件数y(件) | 30 | 40 | 60 | 50 | 70 |
(1)画散点图;
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为89个,那么机器的运转速度应控制在什么范围内?(参考数值:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2﹣alnx﹣bx(a>0).
(Ⅰ)若a=1,b=3,求函数y=f(x)在(1,f(1))处的切线方程;
(Ⅱ)若f(x1)=f(x2)=0,且x1≠x2,证明:f′(![]() )>0.
)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂共有男女员工500人,现从中抽取100位员工对他们每月完成合格产品的件数统计如下:
每月完成合格产品的件数(单位:百件) |
|
|
|
|
|
频数 | 10 | 45 | 35 | 6 | 4 |
男员工人数 | 7 | 23 | 18 | 1 | 1 |
(1)其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面![]() 列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
非“生产能手” | “生产能手” | 合计 | |
男员工 | |||
女员工 | |||
合计 |
(2)为提高员工劳动的积极性,工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的,计件单价为1元;超出![]() 件的部分,累进计件单价为1.2元;超出
件的部分,累进计件单价为1.2元;超出![]() 件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
附:![]() ,
,
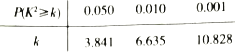 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C的离心率为![]() ,且椭圆C过点
,且椭圆C过点![]() .
.
(1)求椭圆C的标准方程:
(2)若直线l:![]() 与椭圆C相交于A,B两点(A,B不是左右顶点),且以
与椭圆C相交于A,B两点(A,B不是左右顶点),且以![]() 为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的是( )
A. 回归直线一定过样本中心![]()
B. 残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C. 两个模型中残差平方和越小的模型拟合的效果越好
D. 甲、乙两个模型的![]() 分别约为0.98和0.80,则模型乙的拟合效果更好
分别约为0.98和0.80,则模型乙的拟合效果更好
查看答案和解析>>
科目:高中数学 来源: 题型:
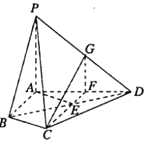
【题目】如图所示四棱锥P-ABCD平面![]() ,E为线段BD上的一点,且EB=ED=EC=BC,连接CE并延长交AD于F
,E为线段BD上的一点,且EB=ED=EC=BC,连接CE并延长交AD于F
(1)若G为PD的中点,求证:平面![]() 平面CGF;
平面CGF;
(2)若BC=2,PA=3,求平面BCP与平面DCP所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com