
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,且离心率为
,且离心率为![]() ,圆
,圆![]() .
.
(1)求椭圆C的方程,
(2)点P在圆D上,F为椭圆右焦点,线段PF与椭圆C相交于Q,若![]() ,求
,求![]() 的取值范围.
的取值范围.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
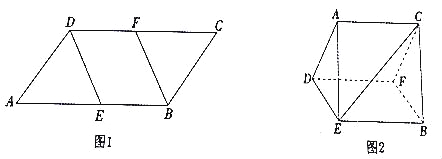
【题目】如图1,在平行四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,分别沿
的中点,分别沿![]() .
.![]() 将
将![]() 和
和![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (点
(点![]() 在平面
在平面![]() 的同侧),连接
的同侧),连接![]() ,如图2所示.
,如图2所示.
(1)求证:![]() ;
;
(2)当![]() ,且平面
,且平面![]() 平面
平面![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 分别与直线
分别与直线![]() ,
,![]() 交于
交于![]() ,其中点
,其中点![]() 在第三象限,点
在第三象限,点![]() 在第二象限,点
在第二象限,点![]() ;
;
(1)若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)直线![]() 交于
交于![]() 点
点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,若
,若![]() 直线的斜率均存在,分别设为
直线的斜率均存在,分别设为![]() ,判断
,判断![]() 是否为定值?若为定值,求出该定值;若不为定值,说明理由.
是否为定值?若为定值,求出该定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查民众对国家实行“新农村建设”政策的态度,现通过网络问卷随机调查了年龄在20周岁至80周岁的100人,他们年龄频数分布和支持“新农村建设”人数如下表:

(1)根据上述统计数据填下面的2×2列联表,并判断是否有95%的把握认为以50岁为分界点对“新农村建设”政策的支持度有差异;

(2)为了进一步推动“新农村建设”政策的实施,中央电视台某节目对此进行了专题报道,并在节目最后利用随机拨号的形式在全国范围内选出4名幸运观众(假设年龄均在20周岁至80周岁内),给予适当的奖励.若以频率估计概率,记选出4名幸运观众中支持“新农村建设”人数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:

参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是面
分别是面![]() ,面
,面![]() ,面
,面![]() 的中心,
的中心,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?如果存在,请求出
?如果存在,请求出![]() 的长度;如果不存在,求说明理由.
的长度;如果不存在,求说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(Ⅰ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电力公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行综合排序,综合排序高者中标.
分值权重表如下:
总分 | 技术 | 商务 | 报价 |
100% | 50% | 10% | 40% |
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的.报价表则相对灵活,报价标的评分方法是:基准价的基准分是68分,若报价每高于基准价1%,则在基准分的基础上扣0.8分,最低得分48分;若报价每低于基准价1%,则在基准分的基础上加0.8分,最高得分为80分.若报价低于基准价15%以上(不含15%)每再低1%,在80分在基础上扣0.8分.
在某次招标中,若基准价为1000(万元).甲、乙两公司综合得分如下表:
公司 | 技术 | 商务 | 报价 |
甲 | 80分 | 90分 | A甲分 |
乙 | 70分 | 100分 | A乙分 |
甲公司报价为1100(万元),乙公司的报价为800(万元)则甲,乙公司的综合得分,分别是( )
A. 73,75.4B. 73,80C. 74.6,76D. 74.6,75.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com