
【题目】已知曲线![]() ,问是否存在实数a,使得经过点(1,a)能够作出该曲线的两条切线?若存在求出实数a的取值范围,若不存在,说明理由.
,问是否存在实数a,使得经过点(1,a)能够作出该曲线的两条切线?若存在求出实数a的取值范围,若不存在,说明理由.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图表示的算法功能是( )
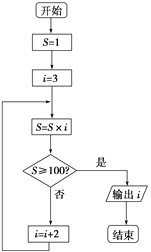
A. 计算小于100的奇数的连乘积
B. 计算从1开始的连续奇数的连乘积
C. 从1开始的连续奇数的连乘积,当乘积大于或等于100时,计算奇数的个数
D. 计算1×3×5×…×n≥100时的最小的n的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=a,其前n项和为Sn , 且满足Sn+Sn﹣1=3n2+2n+4(n≥2),若对任意的n∈N* , an<an+1恒成立,则a的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 【2016高考新课标Ⅲ文数】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() 分别交
分别交![]() 于
于![]() 两点,交
两点,交![]() 的准线于
的准线于![]() 两点.
两点.
(I)若![]() 在线段
在线段![]() 上,
上,![]() 是
是![]() 的中点,证明
的中点,证明![]() ;
;
(II)若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考山东文数】已知椭圆C:![]() (a>b>0)的长轴长为4,焦距为2
(a>b>0)的长轴长为4,焦距为2![]() .
.
(I)求椭圆C的方程;
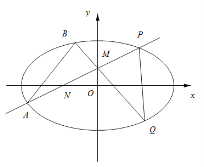
(Ⅱ)过动点M(0,m)(m>0)的直线交x轴与点N,交C于点A,P(P在第一象限),且M是线段PN的中点.过点P作x轴的垂线交C于另一点Q,延长线QM交C于点B.
(i)设直线PM、QM的斜率分别为k、k',证明![]() 为定值.
为定值.
(ii)求直线AB的斜率的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考天津文数】某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:
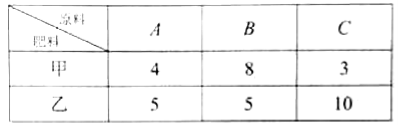
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y计划表示生产甲、乙两种肥料的车皮数.
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(其中ω>0|φ|< ![]() )图象相邻对称轴的距离为
)图象相邻对称轴的距离为 ![]() ,一个对称中心为(﹣
,一个对称中心为(﹣ ![]() ,0),为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
,0),为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
A.向右平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向左平移 ![]() 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com