已知平面向量 ,
,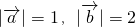 ,且
,且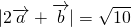 ,则向量
,则向量 与
与 的夹角为________.
的夹角为________.

分析:由条件求得

=

,计算

•(

)=0,可得

⊥(

),从而求得向量

与

的夹角.
解答:因为
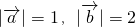
,
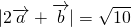
.
∴
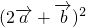
=4

+4

+b
2=4+4

+4=10,
∴

=

.
∴

•(

)=

-2

=1-1=0,
∴

⊥(

),故向量

与

的夹角为

,
故答案为

.
点评:本题主要考查两个向量的数量积的性质以及运算律,两个向量的夹角公式,两个向量垂直的性质,属于基础题.
练习册系列答案
相关习题
科目:高中数学
来源:2013-2014学年广东省中山市一中高三上学期第二次统测理科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2015届广东省佛山市高一下学期期中考试数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2012-2013学年北京市高三阶段考试(二)文科数学试卷(解析版)
题型:选择题
已知平面向量 ,
, ,且
,且 ,则
,则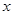 的值为( )
的值为( )
A.-3
B.-1 C.1 D.3
查看答案和解析>>
科目:高中数学
来源:2014届北京市朝阳区高一下学期期末统一考试数学试卷(解析版)
题型:选择题
已知平面向量 ,
, ,且
,且 ,则
,则 的值为
的值为
A. 1 B.
-1 C. 4 D.
-4
查看答案和解析>>
科目:高中数学
来源:2014届浙江省高一下学期期中考试数学试卷(解析版)
题型:填空题
查看答案和解析>>

 ,
,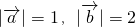 ,且
,且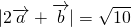 ,则向量
,则向量 与
与 的夹角为________.
的夹角为________.