
【题目】选修4-5:不等式选讲
已知集合![]()
![]() ,对于集合
,对于集合![]() 的两个非空子集
的两个非空子集![]() ,
,![]() ,若
,若![]() ,则称
,则称![]() 为集合
为集合![]() 的一组“互斥子集”.记集合
的一组“互斥子集”.记集合![]() 的所有“互斥子集”的组数为
的所有“互斥子集”的组数为![]() (视
(视![]() 与
与![]() 为同一组“互斥子集”).
为同一组“互斥子集”).
(1)写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() .
.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 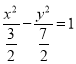
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1经过点A(﹣3,0),B(3,2),直线l2经过点B,且l1⊥l2 .
(1)求经过点B且在两坐标轴上的截距相等的直线的方程;
(2)设直线l2与直线y=8x的交点为C,求△ABC外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了丰富退休生活,老王坚持每天健步走,并用计步器记录每天健步走的步数.他从某月中随机抽取20天的健步走步数(老王每天健步走的步数都在![]() 之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
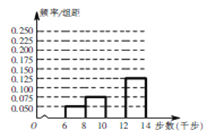
(1)完成频率分布直方图,并估计该月老王每天健步走的平均步数(每组数据可用区间中点值代替;
(2)某健康组织对健步走步数的评价标准如下表:
每天步数分组(千步) |
|
|
|
评价级别 | 及格 | 良好 | 优秀 |
现从这20天中评价级别是“及格”或“良好”的天数里随机抽取2天,求这2天的健步走结果属于同一评价级别的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,![]() 为前
为前![]() 天两只老鼠打洞之和,则
天两只老鼠打洞之和,则![]() _________________尺.
_________________尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如表:
的影响,对近五年该农产品的年产量和价格统计如表:
| 1 | 2 | 3 | 4 | 5 |
| 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润![]() 取到最大值?(保留两位小数)
取到最大值?(保留两位小数)
参考公式: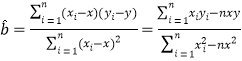 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中,若截面PQMN是正方形,则在下列命题中,错误的为( ) 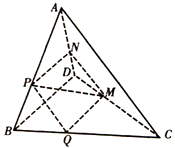
A.AC⊥BD
B.AC=BD
C.AC∥截面PQMN
D.异面直线PM与BD所成的角为45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com