
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)当![]() 时,
时,![]() ,然后根据对数底数大于
,然后根据对数底数大于![]() 的图象性质可得
的图象性质可得![]() ,解之即可得到答案;(2)根据题意可得
,解之即可得到答案;(2)根据题意可得![]() ,变形后为
,变形后为![]() ,然后将
,然后将![]() 的值代入求解
的值代入求解![]() 的值后进一步结合
的值后进一步结合![]() 的取值范围分析
的取值范围分析![]() 的取值范围;(3)首先可以假设当
的取值范围;(3)首先可以假设当![]() 时,则
时,则![]() ,故有
,故有![]() ,判断出函数的单调性,可设函数
,判断出函数的单调性,可设函数![]() 在区间
在区间![]() 上的最大值与最小值分别为
上的最大值与最小值分别为![]() ,令其两者之差不小于
,令其两者之差不小于![]() 列出不等式,解不等式即可.
列出不等式,解不等式即可.
试题解析:(1)由![]() ,得
,得![]() ,
,
解得![]() .
.
(2)![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,经检验,满足题意.
,经检验,满足题意.
当![]() 时,
时,![]() ,经检验,满足题意.
,经检验,满足题意.
当![]() 且
且![]() 时,
时,![]() ,
,![]() ,
,![]() .
.
![]() 是原方程的解当且仅当
是原方程的解当且仅当![]() ,即
,即![]() ;
;
![]() 是原方程的解当且仅当
是原方程的解当且仅当![]() ,即
,即![]() .
.
于是满足题意的![]() .
.
综上,![]() 的取值范围为
的取值范围为![]() .
.
(3)当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
函数![]() 在区间
在区间![]() 上的最大值与最小值分别为
上的最大值与最小值分别为![]() ,
,![]() .
.
![]() 即
即![]() ,对任意
,对任意
![]() 成立.
成立.
因为![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() 时,
时,![]()
有最小值![]() ,由
,由![]() ,得
,得![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)估计用电量落在[220,300)中的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆C的圆心在直线l:y=2x﹣4上,半径为1,点A(0,3). (Ⅰ)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(Ⅱ)若圆C上存在点M,使|MA|=2|MO|(O为坐标原点),求圆心C的横坐标a的取值范围.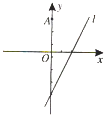
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(第x周)和市场占有率(y﹪)的几组相关数据如下表:
| 1 | 2 | 3 | 4 | 5 |
| 0.03 | 0.06 | 0.1 | 0.14 | 0.17 |
(Ⅰ)根据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)根据上述线性回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测在第几周,该款旗舰机型市场占有率将首次超过 0.40﹪(最后结果精确到整数).
参考公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图像如图所示,将
的部分图像如图所示,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
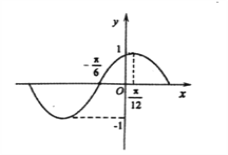
(1)求函数![]() 的解析式;
的解析式;
(2)在![]() 中,角A,B,C满足
中,角A,B,C满足![]() ,且其外接圆的半径R=2,求
,且其外接圆的半径R=2,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com