
【题目】已知定义在![]() 上的数
上的数![]() 满足
满足![]() ,当
,当![]() 时
时![]() .若关于
.若关于![]() 的方程
的方程![]() 有三个不相等的实数根,则实数
有三个不相等的实数根,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
根据f(2﹣x)=f(2+x)可知函数f(x)关于x=2对称,利用当![]() 时
时![]() ,画出函数y=f(x)的大致图象.由题意转化为y=k(x﹣2)+e﹣1与f(x)有三个交点,直线恒过定点(2,e﹣1),再根据数形结合法可得k的取值范围.
,画出函数y=f(x)的大致图象.由题意转化为y=k(x﹣2)+e﹣1与f(x)有三个交点,直线恒过定点(2,e﹣1),再根据数形结合法可得k的取值范围.
由题意,当x≤2时,f(x)=(x﹣1)ex﹣1.f′(x)=xex.
①令f′(x)=0,解得x=0;②令f′(x)<0,解得x<0;③令f′(x)>0,解得0<x≤2.
∴f(x)在(﹣∞,0)上单调递减,在(0,2]上单调递增,
在x=0处取得极小值f(0)=﹣2.且f(1)=﹣1;x→﹣∞,f(x)→0.
又∵函数f(x)在R上满足f(2﹣x)=f(2+x),∴函数f(x)的图象关于x=2对称.
∴函数y=f(x)的大致图象如图所示:

关于x的方程f(x)﹣kx+2k﹣e+1=0可转化为f(x)=k(x﹣2)+e﹣1.
而一次函数y=k(x﹣2)+e﹣1很明显是恒过定点(2,e﹣1).结合图象,当k=0时,有两个交点,不符合题意,
当k=e时,有两个交点,其中一个是(1,﹣1).此时y=f(x)与y=k(x﹣2)+e﹣1正好相切.
∴当0<k<e时,有三个交点.同理可得当﹣e<k<0时,也有三个交点.
实数k的取值范围为:(﹣e,0)∪(0,e).
故选:D.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】为了解某市公益志愿者的年龄分布情况,有关部门通过随机抽样,得到如图1的频率分布直方图.
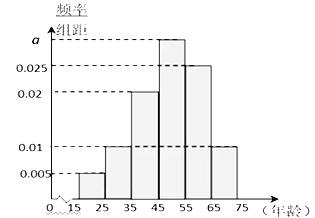
(1)求a的值,并估计该市公益志愿者年龄的平均数(同一组中的数据用该组区间的中点值作代表);
(2)根据世界卫生组织确定新的年龄分段,青年是指年龄15~44岁的年轻人.据统计,该市人口约为300万人,其中公益志愿者约占总人口的40%.试根据直方图估计该市青年公益志愿者的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的![]() 点处,乙船在中间
点处,乙船在中间![]() 点处,丙船在最后面的
点处,丙船在最后面的![]() 点处,且
点处,且![]() .一架无人机在空中的
.一架无人机在空中的![]() 点处对它们进行数据测量,在同一时刻测得
点处对它们进行数据测量,在同一时刻测得![]() ,
, ![]() .(船只与无人机的大小及其它因素忽略不计)
.(船只与无人机的大小及其它因素忽略不计)

(1)求此时无人机到甲、丙两船的距离之比;
(2)若此时甲、乙两船相距100米,求无人机到丙船的距离.(精确到1米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有1000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族",计划在明年及明年以后才购买5G手机的员工称为“观望者”,调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
(1)完成下列![]() 列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
属于“追光族" | 属于“观望者" | 合计 | |
女性员工 | |||
男性员工 | |||
合计 | 100 |
(2)已知被抽取的这100名员工中有10名是人事部的员工,这10名中有3名属于“追光族”.现从这10名中随机抽取3名,记被抽取的3名中属于“追光族”的人数为随机变量X,求![]() 的分布列及数学期望.
的分布列及数学期望.
附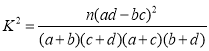 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | p>0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解学生假期参与志愿服务活动的情况,随机调查了![]() 名男生,
名男生,![]() 名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
超过 | 不超过 | |
男 |
|
|
女 |
|
|
(1)能否有![]() 的把握认为该校学生一周参与志愿服务活动时间是否超过
的把握认为该校学生一周参与志愿服务活动时间是否超过![]() 小时与性别有关?
小时与性别有关?
(2)以这![]() 名学生参与志愿服务活动时间超过
名学生参与志愿服务活动时间超过![]() 小时的频率作为该事件发生的概率,现从该校学生中随机抽查
小时的频率作为该事件发生的概率,现从该校学生中随机抽查![]() 名学生,试估计这
名学生,试估计这![]() 名学生中一周参与志愿服务活动时间超过
名学生中一周参与志愿服务活动时间超过![]() 小时的人数.
小时的人数.
附:
|
|
|
|
|
|
|
|
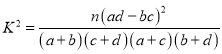
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( ).
①在![]() 中,若
中,若![]() ,则
,则![]() 是等腰三角形;
是等腰三角形;
②在![]() 中,若
中,若 ![]() ,则
,则![]()
③两个向量![]() ,
,![]() 共线的充要条件是存在实数
共线的充要条件是存在实数![]() ,使
,使![]()
④等差数列的前![]() 项和公式是常数项为0的二次函数.
项和公式是常数项为0的二次函数.
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com