
【题目】如图在棱锥P﹣ABCD中,ABCD为矩形,PD⊥面ABCD,PB=2,PB与面PCD成45°角,PB与面ABD成30°角. 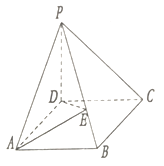
(1)在PB上是否存在一点E,使PC⊥面ADE,若存在确定E点位置,若不存在,请说明理由;
(2)当E为PB中点时,求二面角P﹣AE﹣D的余弦值.
【答案】
(1)解:法一:要证明PC⊥面ADE,易知AD⊥面PDC,即得AD⊥PC,故只需 ![]() 即可,
即可,
所以由 ![]() ,即存在点E为PC中点
,即存在点E为PC中点
法二:建立如图所示的空间直角坐标系D﹣XYZ,
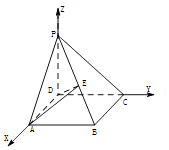
由题意知PD=CD=1, ![]() ,设
,设 ![]() ,∴
,∴ ![]() ,
, ![]()
由 ![]() ,得
,得 ![]() ,
,
即存在点E为PC中点
(2)解:由(1)知D(0,0,0), ![]() ,
, 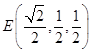 ,P(0,0,1)
,P(0,0,1) ![]() ,
, 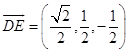 ,
, ![]() ,
, 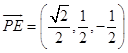
设面ADE的法向量为 ![]() ,面PAE的法向量为
,面PAE的法向量为 ![]()
由的法向量为 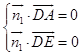 得,
得, 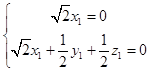 得
得 ![]()
同理求得 ![]() 所以
所以 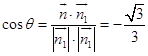
故所求二面角P﹣AE﹣D的余弦值为 ![]() .
.
【解析】(1)法一:要证明PC⊥面ADE,只需证明AD⊥PC,通过证明 ![]() 即可,然后推出存在点E为PC中点.法二:建立如图所示的空间直角坐标系D﹣XYZ,设
即可,然后推出存在点E为PC中点.法二:建立如图所示的空间直角坐标系D﹣XYZ,设 ![]() ,通过
,通过 ![]() =0得到
=0得到 ![]() ,即存在点E为PC中点. (2)由(1)知求出面ADE的法向量,面PAE的法向量,利用空间向量的数量积.求解二面角P﹣AE﹣D的余弦值.
,即存在点E为PC中点. (2)由(1)知求出面ADE的法向量,面PAE的法向量,利用空间向量的数量积.求解二面角P﹣AE﹣D的余弦值.
【考点精析】根据题目的已知条件,利用直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x在区间[2,3]上单调递增,则实数a的取值范围是( )
A.[﹣2,+∞)
B.[﹣3,+∞)
C.[0,+∞)
D.(﹣∞,﹣2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场进行有奖促销活动,顾客购物每满500元,可选择返回50元现金或参加一次抽奖,抽奖规则如下:从1个装有6个白球、4个红球的箱子中任摸一球,摸到红球就可获得100元现金奖励,假设顾客抽奖的结果相互独立.
(Ⅰ)若顾客选择参加一次抽奖,求他获得100元现金奖励的概率;
(Ⅱ)某顾客已购物1500元,作为商场经理,是希望顾客直接选择返回150元现金,还是选择参加3次抽奖?说明理由;
(Ⅲ)若顾客参加10次抽奖,则最有可能获得多少现金奖励?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形OABC边长为3,点M,N分别为线段BC,AB上一点,且2BM=MC,AN=NB,P为△BNM内一点(含边界),设 ![]() (λ,μ为实数),则
(λ,μ为实数),则 ![]() 的最大值为
的最大值为 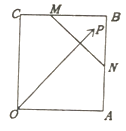
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域均为D的三个函数f(x),g(x),h(x)满足条件:对任意x∈D,点(x,g(x)与点(x,h(x)都关于点(x,f(x)对称,则称h(x)是g(x)关于f(x)的“对称函数”.已知g(x)= ![]() ,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是
,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,AC=1, ![]() ,设∠BAC=x,记
,设∠BAC=x,记 ![]() ;
;
(1)求函数f(x)的解析式及定义域;
(2)试写出函数f(x)的单调递增区间,并求方程 ![]() 的解.
的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足不等式组  ,若目标函数z=kx+y仅在点(1,1)处取得最小值,则实数k的取值范围是 ( )
,若目标函数z=kx+y仅在点(1,1)处取得最小值,则实数k的取值范围是 ( )
A.(﹣1,+∞)
B.(﹣∞,﹣1)
C.(1,+∞)
D.(﹣∞,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com