
����Ŀ��ij�ؽ�����Ϊ�˼�鱾�ؼס�������ѧУ��ѧ����ȫ֪ʶ��ѧϰ�������������ѧУ�����˰�ȫ֪ʶ���ԣ������������ѧУ����ȡ20��ѧ���Ŀ��Գɼ���Ϊ�������ɼ����ڻ����80�ֵ�Ϊ���㣬����Ϊ�����㣬ͳ�ƽ������ͼ��
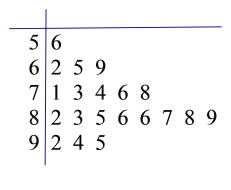
��У ��У
��1������У�ɼ������ѧ������ѡ��������������ѧ���ijɼ�ǡ��һ������![]() �ڵĸ��ʣ�
�ڵĸ��ʣ�
��2������������������������������ش��ܷ��ڷ����ĸ��ʲ�����0.1��ǰ������Ϊѧ���ijɼ�������ѧУ��ѡ���йء�
��У | ��У | �ܼ� | |
���� | |||
������ | |||
�ܼ� |
![]()
����� | P��K2��k0�� | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | span>3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡�(1) ![]() .
.
(2)���������������ڷ����ĸ��ʲ�����0.1��ǰ������Ϊѧ���ijɼ�������ѧУ��ѡ���й�.
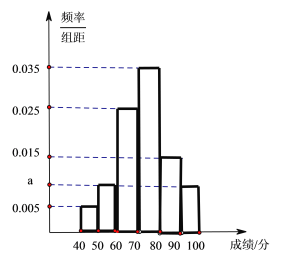
����������������1������Ƶ�ʺ�Ϊ![]() �����
�����![]() ��ֵ���ټ�����У�ɼ������ѧ�����������оٷ��������У�ɼ������ѧ������ѡ�����Ļ����¼�������Ϊ
��ֵ���ټ�����У�ɼ������ѧ�����������оٷ��������У�ɼ������ѧ������ѡ�����Ļ����¼�������Ϊ![]() ������ѧ���ijɼ�ǡ��һ������
������ѧ���ijɼ�ǡ��һ������![]() �ڵĻ����¼��ĸ���Ϊ
�ڵĻ����¼��ĸ���Ϊ![]() �����ùŵ�����ʹ�ʽ�ɵý��. ��2�����������������ݣ����ù�ʽ
�����ùŵ�����ʹ�ʽ�ɵý��. ��2�����������������ݣ����ù�ʽ![]() ���
���![]() ���Ӷ��ɵý��.
���Ӷ��ɵý��.
�������1����Ƶ�ʷֲ�ֱ��ͼ�о������Ϊ1
![]()
![]()
�ɼ�����![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]()
�ɼ�����![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]()
����У�ɼ������ѧ������ѡ�����Ļ����¼�������Ϊ![]()
����ѧ���ijɼ�ǡ��һ������![]() �ڵĻ����¼��ĸ���Ϊ
�ڵĻ����¼��ĸ���Ϊ![]()
��������ѧ���ijɼ�ǡ��һ������![]() �ڵĸ���Ϊ��
�ڵĸ���Ϊ��![]()
��2������֪������������
��У | ��У | �ܼ� | |
���� | 11 | 5 | 16 |
������ | 9 | 15 | 24 |
�ܼ� | 20 | 20 | 40 |
![]()
![]()
![]()
![]() �����ڷ����ĸ��ʲ�����0.1��ǰ������Ϊѧ���ijɼ�������ѧУ��ѡ���й�.
�����ڷ����ĸ��ʲ�����0.1��ǰ������Ϊѧ���ijɼ�������ѧУ��ѡ���й�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ�����ϡ��С���ְ��430��,��������ְ��160�ˣ�����ְ������������ְ��������2����Ϊ�˽�ְ������״�����ֲ��÷ֲ�����������е��飬�ڳ�ȡ��������������ְ��32�ˣ���������е�����ְ������Ϊ
A. 9 B. 18 C. 27 D. 36
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ÿ���Լ������ϰ࣬����·�����õ�ʱ��![]() �����ӣ����·��ӵ������й�.С����һ���������¼��200���ϰ���·�����õ�ʱ�䣬��Ƶ��ͳ�����±�����Ƶ�ʽ��ƴ������.
�����ӣ����·��ӵ������й�.С����һ���������¼��200���ϰ���·�����õ�ʱ�䣬��Ƶ��ͳ�����±�����Ƶ�ʽ��ƴ������.
| 15 | 20 | 25 | 30 |
Ƶ�����Σ� | 50 | 50 | 60 | 40 |
������С���ϰ���·������ʱ�����ѧ����![]() ��
��
������С��һ���ϰ�5�죬ÿ��ĵ�·ӵ������˴˶�������һ�����ϰ���·������ʱ�䲻����![]() ������Ϊ
������Ϊ![]() ����
����![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1����![]() ʱ������
ʱ������![]() �ĵ����������䣻
�ĵ����������䣻
��2������![]() ��
��![]() Ϊ����ʵ��������
Ϊ����ʵ��������![]() �ķ���
�ķ���![]() ǡ������������ʵ������ʵ��
ǡ������������ʵ������ʵ��![]() ��ֵ��
��ֵ��
��3���ڣ�2���������£�������ʽ![]() ��
��![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b������ ![]() ��ȡֵ������
��ȡֵ������ ![]() ��R�����������켫ֵ��ĸ����ǣ� ��
��R�����������켫ֵ��ĸ����ǣ� ��
A.![]()
B.1- ![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ������
������
(1)��![]() ������
������![]() �ļ�ֵ��
�ļ�ֵ��
(2)������![]() ��
��![]() �ϵ�����������ʵ��
�ϵ�����������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��x0 �� 0����B��0��y0������ֱ���x���y�����˶�����|AB|=1��������P��x��y������ ![]() ��
��
��1���������P�Ĺ켣��Ӧ����C�ı����̣�
��2��һ���ݽؾ�Ϊ2��ֱ��l1������C����P��Q���㣬����PQֱ����Բǡ��ԭ�㣬���ֱ�߷��̣�
��3��ֱ��l2��x=ty+1������C����A��B���㣬E��1��0�������ʣ���t�仯ʱ���Ƿ����һֱ��l2 �� ʹ��ABE�����Ϊ ![]() �������ڣ����ֱ��l2�ķ��̣��������ڣ�˵�����ɣ�
�������ڣ����ֱ��l2�ķ��̣��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����С��1�ĵȱ�����{an}��ǰn���ΪSn �� a1= ![]() ����13a2=3S3��n��N*����
����13a2=3S3��n��N*����
��1��������{an}��ͨ�ʽ��
��2����bn=log3��1��Sn+1������ ![]() +
+ ![]() +��+
+��+ ![]() =
= ![]() ����n��
����n��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2=2x�����㣨2��0����ֱ��l��C��A��B���㣬ԲM�����߶�ABΪֱ����Բ��
����֤��������ԭ��O��ԲM�ϣ�
������ԲM����P��4����2������ֱ��l��ԲM�ķ��̣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com