
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】流行性感冒多由病毒引起,据调查,空气相对湿度过大或过小时,都有利于一些病毒的繁殖和传播.科学测定,当空气相对湿度大于65%或小于40%时,病毒繁殖滋生较快,当空气相对湿度在45%—55%时,病毒死亡较快,现随机抽取了全国部分城市,获得了它们的空气月平均相对湿度共300个数据,整理得到数据分组及频数分布表,其中为了记录方便,将空气相对湿度在![]() %~
%~![]() %时记为区间
%时记为区间![]() .
.

(I)求上述数据中空气相对湿度使病毒死亡较快的频率;
(Ⅱ)从区间[ 15,35)的数据中任取两个数据,求恰有一个数据位于[25,35)的概率;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中空气月平均相对湿度的平均数在第几组(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=A cos(ωx+φ)(A>0,ω>0)的部分图象如图所示,下面结论错误的是( )

A. 函数f(x)的最小正周期为![]()
B. 函数f(x)的图象可由g(x)=Acos ωx的图象向右平移![]() 个单位长度得到
个单位长度得到
C. 函数f(x)的图象关于直线x=![]() 对称
对称
D. 函数f(x)在区间![]() 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 同时满足条件:①存在互异的
同时满足条件:①存在互异的![]() 使得
使得![]() (
(![]() 为常数);
为常数);
②当![]() 且
且![]() 时,对任意
时,对任意![]() 都有
都有![]() ,则称数列
,则称数列![]() 为双底数列.
为双底数列.
(1)判断以下数列![]() 是否为双底数列(只需写出结论不必证明);
是否为双底数列(只需写出结论不必证明);
①![]() ; ②
; ②![]() ; ③
; ③![]()
(2)设![]() ,若数列
,若数列![]() 是双底数列,求实数
是双底数列,求实数![]() 的值以及数列
的值以及数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,是否存在整数
,是否存在整数![]() ,使得数列
,使得数列![]() 为双底数列?若存在,求出所有的
为双底数列?若存在,求出所有的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为3的等边三角形,四边形
是边长为3的等边三角形,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .点
.点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() ,点
,点![]() 为
为![]() 上的一点,且
上的一点,且![]() .
.

(Ⅰ)当![]() 时,求证:
时,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,在《我是演说家》第四季这档节目中,英国华威大学留学生游斯彬的“数学之美”的演讲视频在微信朋友圈不断被转发,他的视角独特,语言幽默,给观众留下了深刻的印象.某机构为了了解观众对该演讲的喜爱程度,随机调查了观看了该演讲的140名观众,得到如下的列联表:(单位:名)
男 | 女 | 总计 | |
喜爱 | 40 | 60 | 100 |
不喜爱 | 20 | 20 | 40 |
总计 | 60 | 80 | 140 |
(1)根据以上列联表,问能否在犯错误的概率不超过0.05的前提下认为观众性别与喜爱该演讲有关.(精确到0.001)
(2)从这60名男观众中按对该演讲是否喜爱采取分层抽样,抽取一个容量为6的样本,然后随机选取两名作跟踪调查,求选到的两名观众都喜爱该演讲的概率.
附:临界值表
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.705 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下四种变换方式:
① 向左平移![]() 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的![]() ;
;
② 向右平移![]() 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的![]() ;
;
③ 每个点的横坐标缩短为原来的![]() ,向右平移
,向右平移![]() 个单位长度;
个单位长度;
④ 每个点的横坐标缩短为原来的![]() ,向左平移
,向左平移![]() 个单位长度;
个单位长度;
其中能将![]() 的图像变换成函数
的图像变换成函数![]() 的图像的是( )
的图像的是( )
A.①和③ B.①和④ C.②和④ D.②和③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某几何体![]() 中,四边形
中,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形, ![]() 是直角梯形,
是直角梯形, ![]() 是直角,
是直角, ![]() ,
, ![]() 是以
是以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, ![]() .
.
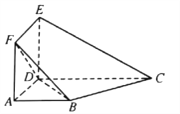
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com