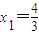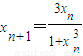练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    对数列{xn}，满足，；对函数f（x）在（-2，2）上有意义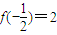，，且满足x，y，z∈（-2，2）时，有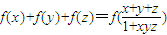成立，则f（xn）的表示式为（ ）
    A．-2n
    B．3n
    C．-2×3n
    D．2×3n
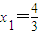    【答案】分析：由，结合已知可得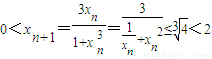．由x=y=z=0可得f（-x）=-f（x）．再根据题设条件能够推出{f（xn）}是以-6为首项，以3为公比的等比数列，由此能够求出f（xn）的表示式．
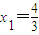    解答：解：由，结合已知可得；
    由x=y=z=0⇒3f（0）=f（0），
    ∴f（0）=0，令z=0，得f（x）+f（y）=f（x+y），
    令y=-x，则f（x）+f（-x）=f（0）=0，
    则f（-x）=-f（x）．
    又=，
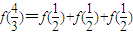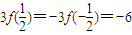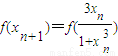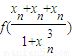    且==f（xn）+f（xn）+f（xn）=3f（xn），
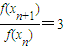    于是，即{f（xn）}是以-6为首项，以3为公比的等比数列，
    所以f（xn）=-2×3n．
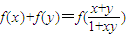    点评：本题考查函数奇偶性、特殊值法应用及递推数列通项公式求法．“函数f（x）在上（-2，2）有意义，满足x，y∈（-2，2）时，有成立，则函数f（x）是奇函数”，这一性质来源于课本习题．本题将其与数列相结合，可谓精工之作．可见，重视课本例、习题很有必要．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    对数列{xn}，满足x1=
    4
    3
    ，xn+1=
    3xn
    1+
    x
    3
    n
    ；对函数f（x）在（-2，2）上有意义，f(-
    1
    2
    )=2    ，且满足x，y，z∈（-2，2）时，有f(x)+f(y)+f(z)=f(
    x+y+z
    1+xyz
    )    成立，则f（xn）的表示式为（　　）
    A、-2n
    B、3n
    C、-2×3n
    D、2×3n

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对数列{xn}，满足x1=
    4
    5
    ，xn+1=
    2xn
    1+
    x
    2
    n
    ；对函数f（x）在（-2，2）上有意义，f(
    1
    2
    )=-2    ，且满足x，y∈（-2，2）时，有f(x)+f(y)=f(
    x+y
    1+xy
    )    成立，则数列{f（xn）}是（　　）
    A、以-4为首项以2为公差的等差数列
    B、以-4为首项以2为公比的等比数列
    C、既是等差数列又是等比数列
    D、既不是等差数列又不是等比数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对数列{xn}，满足x1=
    4
    5
    ，xn+1=
    2xn
    1+
    x
    2
    n
    ；对函数f（x）在上（-1，1）有意义，f(-
    1
    2
    )=2    ，且满足x，y∈（-1，1）时，有f(x)+f(y)=f(
    x+y
    1+xy
    )    成立，则f（xn）的表示式为（　　）
    A、-2n-1
    B、2n
    C、-2n+1
    D、2n+1

    查看答案和解析>>

    科目：高中数学 来源：2010年全国高考数学模拟试卷（1）（解析版） 题型：选择题

    对数列{xn}，满足，；对函数f（x）在上（-1，1）有意义，，且满足x，y∈（-1，1）时，有成立，则f（xn）的表示式为（ ）
    A．-2n-1
    B．2n
    C．-2n+1
    D．2n+1

    查看答案和解析>>

    同步练习册答案