【题目】随着2022年北京冬奥会的临近，中国冰雪产业快速发展，冰雪运动人数快速上升，冰雪运动市场需求得到释放.如图是2012-2018年中国雪场滑雪人数（单位：万人）与同比增长情况统计图则下面结论中正确的是（ ）.
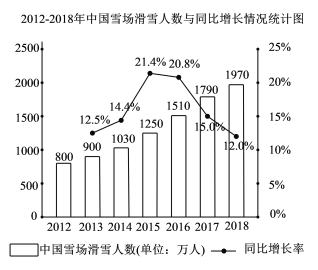
A.2012-2018年，中国雪场滑雪人数逐年增加；
B.2013-2015年，中国雪场滑雪人数和同比增长率均逐年增加；
C.中国雪场2015年比2014年增加的滑雪人数和2018年比2017年增加的滑雪人数均为220万人，因此这两年的同比增长率均有提高；
D.2016-2018年，中国雪场滑雪人数的增长率约为23.4%.
【答案】AB
【解析】
根据条形图判断人数增减性，即可判断A；根据折线图判断同比增长率增减性，即可判断B； 根据折线图判断同比增长率,即可判断C；计算2016-2018年滑雪人数的增长率可判断D.
根据条形图知，2012-2018年，中国雪场滑雪人数逐年增加，所以A正确；
根据条形图知，2013-2015年，中国雪场滑雪人数逐年增加，
根据折线图知，2013-2015年，中国雪场滑雪人数同比增长率逐年增加，所以B正确；
根据条形图知，中国雪场2015年比2014年增加的滑雪人数为
万人，2018年比2017年增加的滑雪人数为
万人，根据折线图知，2015年比2014年同比增长率上升，但2018年比2017年同比增长率有下降，故C错误；
2016-2018年，中国雪场滑雪人数的增长率约为
，故D错误；
故选：AB
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，直线
的参数方程为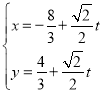
（
为参数）.以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
，其中
.
（Ⅰ）写出直线的普通方程和曲线的直角坐标方程；
（Ⅱ）在平面直角坐标系中，设直线与曲线相交于
，
两点.若点
恰为线段
的三等分点，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知抛物线E：
（
）与圆O：
相交于A，B两点，且
.过劣弧
上的动点
作圆O的切线交抛物线E于C，D两点，分别以C，D为切点作抛物线E的切线
，
，相交于点M.
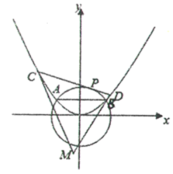
（1）求抛物线E的方程；
（2）求点M到直线
距离的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(本小题满分12分)已知圆
，圆
，动圆
与圆
外切并且与圆
内切，圆心的轨迹为曲线
．
（Ⅰ）求的方程；
（Ⅱ）
是与圆，圆都相切的一条直线，与曲线交于
，
两点，当圆的半径最长时，求
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在①
，②
，③
这三个条件中任选一个，补充在下面问题中，并解答.
已知等比数列
的公比
，前n项和为
，若_________，数列
满足
，
.
（1）求数列，的通项公式；
（2）求数列
的前n项和
，并证明
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
