
����Ŀ��ij�����̳��ֱ��Ƴ�֧����������ɨ��֧�����������������һ��ʱ����ƹ��ڣ������ƹ������Ż����Ƚϴ�����Խ��Խ����˿�ʼʹ����ɨ��֧��������ͳ���˻���Ƴ�һ����ÿ��ʹ��ɨ��֧�����˴Σ���![]() ��ʾ��Ƴ���������
��ʾ��Ƴ���������![]() ��ʾÿ��ʹ��ɨ��֧�����˴Σ�ͳ���������±���ʾ��
��ʾÿ��ʹ��ɨ��֧�����˴Σ�ͳ���������±���ʾ��
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
��1������ɢ��ͼ�жϣ����ƹ����ڣ�ɨ��֧������![]() �ι��ڻ�Ƴ�����
�ι��ڻ�Ƴ�����![]() �Ļع鷽���ʺ���
�Ļع鷽���ʺ���![]() ����ʾ������ûع鷽�̣���Ԥ���Ƴ���
����ʾ������ûع鷽�̣���Ԥ���Ƴ���![]() ��ʹ��ɨ��֧�����˴Σ�
��ʹ��ɨ��֧�����˴Σ�
��2���ƹ��ڽ������̳��Թ˿͵�֧����ʽ����ͳ�ƣ�������±���
֧����ʽ | �ֽ� | ��Ա�� | ɨ�� |
���� |
|
|
|
�̳��涨��ʹ���ֽ�֧���Ĺ˿����Żݣ�ʹ�û�Ա��֧���Ĺ˿�����![]() ���Żݣ�ɨ��֧���Ĺ˿�����Żݣ�����ͳ�ƽ����֪��ʹ��ɨ��֧���Ĺ˿ͣ�����
���Żݣ�ɨ��֧���Ĺ˿�����Żݣ�����ͳ�ƽ����֪��ʹ��ɨ��֧���Ĺ˿ͣ�����![]() ���Żݵĸ���Ϊ
���Żݵĸ���Ϊ![]() ������
������![]() ���Żݵĸ���Ϊ
���Żݵĸ���Ϊ![]() ������
������![]() ���Żݵĸ���Ϊ
���Żݵĸ���Ϊ![]() ������һ���˿�����
������һ���˿�����![]() Ԫ����Ʒ�����������������¼�������Ƶ����������Ӧ�¼������ĸ��ʣ����Ƹù˿�֧����ƽ�������Ƕ��٣�
Ԫ����Ʒ�����������������¼�������Ƶ����������Ӧ�¼������ĸ��ʣ����Ƹù˿�֧����ƽ�������Ƕ��٣�
�ο����ݣ���![]() ��
��![]() ��
��![]() ��
��![]()
�ο���ʽ������һ������![]() ��
��![]() ������
������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��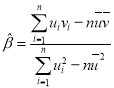 ��
��![]() ��
��
���𰸡���1���ع鷽��Ϊ��![]() ����Ƴ���8��ʹ��ɨ��֧�����˴�Ϊ331��2��һ���˿����ƽ������Ϊ
����Ƴ���8��ʹ��ɨ��֧�����˴�Ϊ331��2��һ���˿����ƽ������Ϊ![]() Ԫ
Ԫ
��������
��1����![]() ������ͬʱȡ���ö����ã�
������ͬʱȡ���ö����ã�![]() ����
����![]() ����
����![]() ��������С���˷����
��������С���˷����![]() ��������ûع鷽�̣��ٽ�
��������ûع鷽�̣��ٽ�![]() ���뷽�̽���Ԥ��ֵ��⣻
���뷽�̽���Ԥ��ֵ��⣻
��2����һ���˿���֧���ķ���Ϊ![]() ��д��
��д��![]() �����п���ȡֵ����������ķֲ��У��Ӷ���ù˿�֧����ƽ������.
�����п���ȡֵ����������ķֲ��У��Ӷ���ù˿�֧����ƽ������.
��1����![]() ������ͬʱȡ���ö����ã�
������ͬʱȡ���ö����ã�![]() ��
��
��![]()
![]()
![]() ��
��![]() ��
��
 ��
��
���������ĵ�![]() ����
����![]() ,��:
,��:![]() ��
��
![]() ��
��
![]()
![]() ����
����![]() �Ļع鷽��Ϊ��
�Ļع鷽��Ϊ��![]() ��
��
��![]() ������ʽ��
������ʽ��![]() ��
��
��Ƴ���8��ʹ��ɨ��֧�����˴�Ϊ331��
��2����һ���˿���֧���ķ���Ϊ![]() ��
��
��![]() ��ȡֵ����Ϊ��
��ȡֵ����Ϊ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]()
�ֲ���Ϊ��
|
|
|
|
|
|
|
|
|
|
���ԣ�һ���˿����ƽ������Ϊ��
![]() ��Ԫ��
��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͨ������ѧ�γ̱���2017�棩���������ѧѧ�Ƶ������������.Ϊ�˱Ƚϼס��������߶�ѧ������ѧ��������ˮƽ��������������Ϊָ��Զ��˽����˲��飬���ݲ������������״�ͼ����ͼ��ÿ��ָ��ֵ����Ϊ5�֣���ֵ����Ϊ�ţ���������������ȷ���ǣ� ��
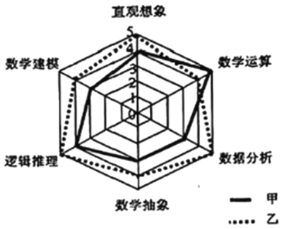
A.�����ݷ�������������
B.����ѧ��ģ����������ѧ��������
C.�ҵ��������������������
D.�ҵ�������������ƽ��ˮƽ���ڼ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
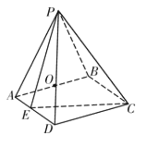
����Ŀ����ͼ���ı���ABCD�DZ߳�Ϊ4�����Σ���BAD=60�㣬�Խ���AC��BD�ཻ�ڵ�O���ı���ACFEΪ���Σ�EF//AC����E��ƽ��ABCD�ϵ���ӰΪOA���е㣬AE��ƽ��ABCD���ɽ�Ϊ45��.
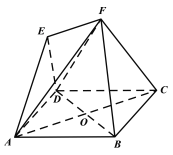
������֤��BD��ƽ��ACF��
������ƽ��DEF��ƽ��ABCD���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P��ABC�У�ƽ��PBC��ƽ��ABC����ACB��90����BC��PC��2����AC��PB��������P��ABC��������ֵΪ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�����꼶������![]() �ˣ�ѧ��Ϊ
�ˣ�ѧ��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ����
��Ů��![]() �ˣ�ѧ��Ϊ
�ˣ�ѧ��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() .�Ը���ѧ�������ʾ����飬��ѧ�Ų���ϵͳ�����ķ���������
.�Ը���ѧ�������ʾ����飬��ѧ�Ų���ϵͳ�����ķ���������![]() ��ѧ���г�ȡ
��ѧ���г�ȡ![]() �˽����ʾ����飨��һ����ü�����������鵽�ĺ���Ϊ
�˽����ʾ����飨��һ����ü�����������鵽�ĺ���Ϊ![]() �����ٴ���
�����ٴ���![]() ��ѧ���������ȡ
��ѧ���������ȡ![]() �˽������ݷ���������
�˽������ݷ���������![]() ���м�����������Ů���ĸ����ǣ� ��
���м�����������Ů���ĸ����ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.��������![]() ����
����![]() ���ķ�����Ϊ������
���ķ�����Ϊ������![]() ����
����![]() ��
��
B.����������![]() ��ʹ��
��ʹ��![]() ���ķ��ǣ���������
���ķ��ǣ���������![]() ������
������![]() ��
��
C.��������![]() ���ձ��ڵ�һ���ǣ���
���ձ��ڵ�һ���ǣ���![]() ����������������Ϊ������
����������������������
D.��֪![]() ��
��![]() �ϵĿɵ�����������
�ϵĿɵ�����������![]() ������
������![]() �Ǻ���
�Ǻ���![]() �ļ�ֵ�����ı�Ҫ���������
�ļ�ֵ�����ı�Ҫ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��
��![]() .
.
��1��������![]() �ڵ�
�ڵ�![]() ����������ֱ��
����������ֱ��![]() ��ֱ����
��ֱ����![]() �ĵ����Ժͼ�Сֵ������
�ĵ����Ժͼ�Сֵ������![]() Ϊ��Ȼ�����ĵ�������
Ϊ��Ȼ�����ĵ�������
��2�����������![]() ��
��![]() ���������
���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() Ϊ�ȱ������Σ�E��F�ֱ�Ϊ
Ϊ�ȱ������Σ�E��F�ֱ�Ϊ![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() .
.
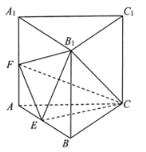
��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵĴ�С.
���ɽǵĴ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У���
����![]() ��
��![]() ������
������![]() ������
������![]() ��
��![]() ��
��![]() ��OΪ
��OΪ![]() ���е㣬��E��
���е㣬��E��![]() �ϣ���
�ϣ���![]() ��
��
��1��֤����![]() ��
��
��2����![]() ���Ƿ����һ��F��ʹ
���Ƿ����һ��F��ʹ![]() ��
��![]() �������ڣ���ȷ����F��λ�ã�
�������ڣ���ȷ����F��λ�ã�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com