
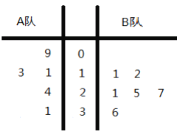
【题目】某电视台举行一个比赛类型的娱乐节目,![]() 两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将
两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将![]() 队第六位选手的成绩没有给出,并且告知大家
队第六位选手的成绩没有给出,并且告知大家![]() 队的平均分比
队的平均分比![]() 队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
(1)主持人从![]() 队所有选手成绩中随机抽取2个,求至少有一个为“晋级”的概率;
队所有选手成绩中随机抽取2个,求至少有一个为“晋级”的概率;
(2)主持人从![]() 两队所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为
两队所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)![]() ;(2)分布列见解析,2.
;(2)分布列见解析,2.
【解析】
(1)先由题意求得![]() 队第六位选手的成绩,则可得
队第六位选手的成绩,则可得![]() 队中成绩不少于21分的有2个,再利用对立事件求概率即可;
队中成绩不少于21分的有2个,再利用对立事件求概率即可;
(2)由(1)可得![]() 队中所有选手成绩能“晋级”的有2个,
队中所有选手成绩能“晋级”的有2个,![]() 队中所有选手成绩能“晋级”的有4个,则
队中所有选手成绩能“晋级”的有4个,则![]() 的可能取值有
的可能取值有![]() ,分别讨论求解即可得到分布列,利用公式求得期望即可
,分别讨论求解即可得到分布列,利用公式求得期望即可
(1)![]() 队选手的平均分为
队选手的平均分为![]() ,
,
设![]() 队第6位选手的成绩为
队第6位选手的成绩为![]() 分,因为
分,因为![]() 队的平均分比
队的平均分比![]() 队的平均分多4分,
队的平均分多4分,
则![]() ,得
,得![]() ,
,
则![]() 队中成绩不少于21分的有2个,
队中成绩不少于21分的有2个,
因为从中抽取2个至少有一个为“晋级”的对立事件为两人都没有“晋级”,
则概率![]()
(2)由(1),![]() 队中所有选手成绩能“晋级”的有2个,
队中所有选手成绩能“晋级”的有2个,![]() 队中所有选手成绩能“晋级”的有4个,则
队中所有选手成绩能“晋级”的有4个,则![]() 的可能取值有
的可能取值有![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
∴![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】近来天气变化无常,陡然升温、降温幅度大于![]() 的天气现象出现增多.陡然降温幅度大于
的天气现象出现增多.陡然降温幅度大于![]() 容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的
容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的![]() 名幼儿进行调查,得到了如下的列联表,若在全部
名幼儿进行调查,得到了如下的列联表,若在全部![]() 名幼儿中随机抽取
名幼儿中随机抽取![]() 人,抽到患伤风感冒疾病的幼儿的概率为
人,抽到患伤风感冒疾病的幼儿的概率为![]() ,
,
(1)请将下面的列联表补充完整;
患伤风感冒疾病 | 不患伤风感冒疾病 | 合计 | |
男 | 25 | ||
女 | 20 | ||
合计 | 100 |
(2)能否在犯错误的概率不超过![]() 的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
(3)已知在患伤风感冒疾病的![]() 名女性幼儿中,有
名女性幼儿中,有![]() 名又患黄痘病.现在从患伤风感冒疾病的
名又患黄痘病.现在从患伤风感冒疾病的![]() 名女性中,选出
名女性中,选出![]() 名进行其他方面的排查,记选出患黄痘病的女性人数为
名进行其他方面的排查,记选出患黄痘病的女性人数为![]() ,求
,求![]() 的分布列以及数学期望.下面的临界值表供参考:
的分布列以及数学期望.下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: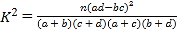 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
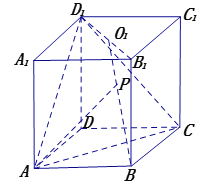
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 且侧棱
且侧棱![]() 其中
其中![]() 为
为![]() 的
的![]() 交点.
交点.
(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)在线段![]() 上,是否存在一个点
上,是否存在一个点![]() ,使得直线
,使得直线![]() 与
与![]() 垂直?若存在,求出线段
垂直?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1260 m,经测量,cos A=![]() ,cos C=
,cos C=![]()
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个不相等的非零向量![]() ,两组向量
,两组向量![]() 和
和![]() 均由2个
均由2个![]() 和3个
和3个![]() 排列而成,记
排列而成,记![]() ,
,![]() 表示
表示![]() 所有可能取值中的最小值,则下列命题中
所有可能取值中的最小值,则下列命题中
(1)![]() 有5个不同的值;(2)若
有5个不同的值;(2)若![]() 则
则![]() 与
与![]() 无关;(3)若
无关;(3)若![]() ,则
,则![]() 与
与![]() 无关;(4)若
无关;(4)若![]() ,则
,则![]() ;(5)若
;(5)若![]() ,
,![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为![]() .正确的是( )
.正确的是( )
A.(1)(2)B.(2)(4)C.(3)(5)D.(1)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了配合今年上海迪斯尼游园工作,某单位设计了统计人数的数学模型![]() :以
:以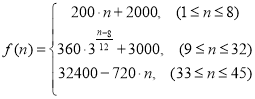 表示第
表示第![]() 个时刻进入园区的人数;以
个时刻进入园区的人数;以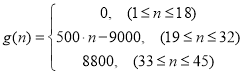 表示第
表示第![]() 个时刻离开园区的人数.设定以
个时刻离开园区的人数.设定以![]() 分钟为一个计算单位,上午
分钟为一个计算单位,上午![]() 点
点![]() 分作为第
分作为第![]() 个计算人数单位,即
个计算人数单位,即![]() ;
;![]() 点
点![]() 分作为第
分作为第![]() 个计算单位,即
个计算单位,即![]() ;依次类推,把一天内从上午
;依次类推,把一天内从上午![]() 点到晚上
点到晚上![]() 点
点![]() 分分成
分分成![]() 个计算单位(最后结果四舍五入,精确到整数).
个计算单位(最后结果四舍五入,精确到整数).
(1)试计算当天![]() 点至
点至![]() 点这一小时内,进入园区的游客人数
点这一小时内,进入园区的游客人数![]() 、离开园区的游客人数
、离开园区的游客人数![]() 各为多少?
各为多少?
(2)假设当日园区游客总人数达到或超过![]() 万时,园区将采取限流措施.该单位借助该数学模型知晓当天
万时,园区将采取限流措施.该单位借助该数学模型知晓当天![]() 点(即
点(即![]() )时,园区总人数会达到最高,请问当日是否要采取限流措施?说明理由.
)时,园区总人数会达到最高,请问当日是否要采取限流措施?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充,已知金字塔的每一条棱和边都相等.
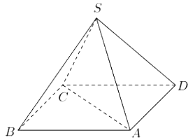
(1)求证:直线AC垂直于直线SD;
(2)若搭边框共使用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() )的最小周期为
)的最小周期为![]() .
.
(1)求![]() 的值及
的值及![]() 的单调递增区间;
的单调递增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标缩短为原来的
个单位,再将图象上各点的横坐标缩短为原来的![]() (纵坐标不变)得到函数
(纵坐标不变)得到函数![]() 的图象,若关于x的方程
的图象,若关于x的方程![]() 在区间
在区间![]() 上有且只有一个解,求实数m的取值范围.
上有且只有一个解,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com