
已知函数 为奇函数,且
为奇函数,且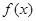 在
在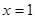 处取得极大值2.
处取得极大值2.
(1)求函数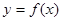 的解析式;
的解析式;
(2)记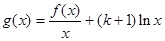 ,求函数
,求函数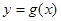 的单调区间。
的单调区间。
解:(1)由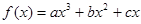 (
( ≠0)为奇函数,
≠0)为奇函数,
∴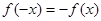 ,代入得,
,代入得,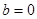 ………………………………………………1分
………………………………………………1分
∴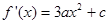 ,且
,且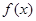 在
在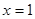 取得极大值2.
取得极大值2.
∴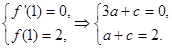 解得
解得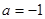 ,
, ,∴
,∴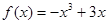 …………4分
…………4分
(2)∵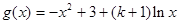 ,定义域为
,定义域为
∴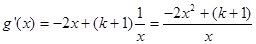 ………………………………………5分
………………………………………5分
1°当 ,即
,即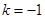 时,
时,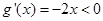 ,函数在
,函数在 上单调递减;………7分
上单调递减;………7分
2°当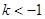 ,
,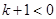 ,∵
,∵ ,∴
,∴
∴函数在 上单调递减; ………………………………………………………9分
上单调递减; ………………………………………………………9分
3°当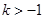 ,
,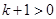 ,令
,令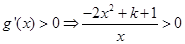 ,∵
,∵ ,
,
∴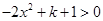 ,解得
,解得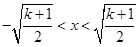 ,结合
,结合 ,得
,得 ……11分[来源:Z。xx。k.Com]
……11分[来源:Z。xx。k.Com]
令 ,解得
,解得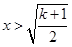 ………………………………………12分
………………………………………12分
∴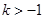 时,函数的单调递增区间为
时,函数的单调递增区间为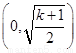 ,递减区间为
,递减区间为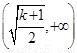 ,………13分
,………13分
综上,当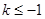 时,函数的单调递减区间为
时,函数的单调递减区间为 ,无单调递增区间,
,无单调递增区间,
当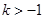 时,函数的单调递增区间为
时,函数的单调递增区间为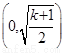 ,递减区间为
,递减区间为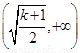 …14分
…14分
【解析】略


科目:高中数学 来源:2013-2014学年山东省等四校高三上学期期中联考理科数学试卷(解析版) 题型:选择题
已知函数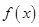 为奇函数,且当
为奇函数,且当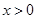 时,
时,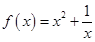 ,则
,则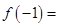 ( )
( )
A.2 B.0 C.1 D.﹣2
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌10所省高三第二次模拟突破冲刺文科数学(二)(解析版) 题型:解答题
已知函数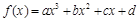 为奇函数,且在
为奇函数,且在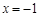 处取得极大值2.
处取得极大值2.
(Ⅰ)求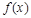 的解析式;
的解析式;
(Ⅱ)过点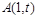 (
(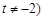 可作函数
可作函数 图像的三条切线,求实数
图像的三条切线,求实数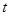 的取值范围;
的取值范围;
(Ⅲ)若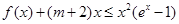 对于任意的
对于任意的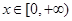 恒成立,求实数
恒成立,求实数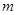 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013届浙江省杭州市金兰合作组织高二下期中文科数学试卷(解析版) 题型:解答题
已知函数 为奇函数,且
为奇函数,且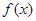 在
在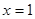 处取得极大值2.(1)求函数
处取得极大值2.(1)求函数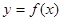 的解析式;
的解析式;
( 2)记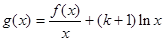 ,求函数
,求函数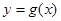 的单调区间;
的单调区间;
(3)在(2)的条件下,当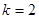 时,若函数
时,若函数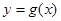 的图像的直线
的图像的直线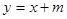 的下方,求
的下方,求 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010-2011年云南省江高二3月月考数学文卷 题型:解答题
(本小题满分12分)
已知函数 为奇函数,
为奇函数, 为偶函数,且
为偶函数,且 .
.
(1)求函数 的解析式;
的解析式;
(2)若存在 ,则称
,则称 是函数
是函数 的一个不动点,求函数
的一个不动点,求函数 的不动点
的不动点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com